Khái niệm:
Thời gian t là thời gian vật tham gia chuyển động từ vị trí này đến vị trí khác theo phương chuyển động của vật.
Đơn vị tính: giây (s), phút (min), giờ (h).
Khái niệm:
Thời gian t là thời gian vật tham gia chuyển động từ vị trí này đến vị trí khác theo phương chuyển động của vật.
Đơn vị tính: giây (s), phút (min), giờ (h).
Chia sẻ qua facebook
Hoặc chia sẻ link trực tiếp:
www.congthucvatly.com/bien-so-thoi-gian-vat-ly-10-17

Bài giảng tổng quan về dao động điều hòa. Biểu diễn vecto quay Fresel. Hệ thức độc lập theo thời gian. Phương trình li độ, vận tốc, gia tốc trong dao động. Video hướng dẫn chi tiết.

Nơi bạn sẽ được học về cách tìm quãng đường lớn nhất hoặc nhỏ nhất của một vật dao động điều hòa.

Video bài giảng hướng dẫn chi tiết cho các bạn hiểu về tốc độ trung bình, vận tốc trung bình trong dao động điều hòa. Kèm theo bài tập ví dụ.

Video hướng dẫn cách giải bài toán tìm thời gian để thỏa một điều kiện cho trước. Có bài tập ví dụ kèm công thức.

Video tổng hợp tất cả các công dụng của vectơ quay Fresnel kèm bài tập áp dụng chi tiết

Video giới thiệu sơ lược về các đặc điểm cơ bản của con lắc lò xo kèm bài tập áp dụng và hướng dẫn chi tiết.

Năng lượng của con lắc lò xo trong dao động điều hòa và định luật bảo toàn năng lượng. Mối quan hệ giữa tần số dao động và tần số của động năng, thế năng.

Trong bài giảng này, chúng ta sẽ cùng nhau tìm hiểu về Sóng cơ học và các định nghĩa cơ bản. Hướng dẫn chi tiết

Chuyển động thẳng nhanh dần đều. Chuyển động chậm dần đều. Chuyển động thẳng biến đổi đều. Hướng dẫn chi tiết.
Tốc độ trung bình được tính bằng quãng đường vật đã đi được chi cho thời gian dịch chuyển. Vận tốc trung bình lại được tính bằng độ dời chia cho thời gian. Từ đây dẫn tới sự khác nhau giữa tốc độ và vận tốc.

Vật lý 10. Chuyển động cơ học là gì? Gốc tọa độ, gốc thời gian, chiều dương, hệ quy chiếu. Chất điểm là gì? Quỹ đạo chuyển động là gì? Tổng hợp công thức và bài giảng liên quan tới chuyển động cơ học.

Trong bài giảng này chúng ta sẽ cùng nhau tìm hiểu về chuyển động thẳng đều. Phương trình của chuyển động thẳng đều. Bài toán xác định vị trí hai xe gặp nhau trong chuyển động thẳng đều. Đồ thị chuyển động thẳng đều.

Thả một hòn đá rơi xuống giếng, sau 4,2s nghe được tiếng động từ dưới giếng vọng lên. Hãy xác định độ sâu của giếng. Biết vận tốc âm thanh trong không khí là 340m/s.

Trong video lần này chúng ta sẽ cùng nhau tìm hiểu về đồ thị của chuyển động thẳng biến đổi đều. Đồ thị gia tốc theo thời gian, đồ thị vận tốc theo thời gian, đồ thị tọa độ theo thời gian.

Vật lý 10. Chuyển động tròn đều. Tốc độ góc, chu kỳ, tần số của chuyển động tròn đều. Vận tốc dài, gia tốc hướng tâm. Video hướng dẫn chi tiết.
Khái niệm:
- Độ dịch chuyển là một vectơ, cho biết độ dài và hướng của sự thay đổi vị trí của vật.
- Độ dịch chuyển được biểu diễn bằng một mũi tên nối vị trí đầu và vị trí cuối của chuyển động, có độ dài tỉ lệ với độ lớn của độ dịch chuyển.
Đơn vị tính: mét (m)
Khái niệm:
Thời gian t là thời gian vật tham gia chuyển động từ vị trí này đến vị trí khác theo phương chuyển động của vật.
Đơn vị tính: giây (s), phút (min), giờ (h).
Khái niệm:
h là độ cao của vật so với điểm làm mốc.
Trong thực tế người ta thường chọn điểm làm mốc (gốc tọa độ) tại mặt đất.
Đơn vị tính: mét .
![]()
Khái niệm:
- Trong Vật lý học, gia tốc trọng trường là gia tốc do lực hấp dẫn tác dụng lên một vật. Bỏ qua ma sát do sức cản không khí, theo nguyên lý tương đương mọi vật nhỏ chịu gia tốc trong một trường hấp dẫn là như nhau đối với tâm của khối lượng.
- Tại các điểm khác nhau trên Trái Đất, các vật rơi với một gia tốc nằm trong khoảng 9,78 và 9,83 phụ thuộc vào độ cao của vật so với mặt đất.
- Trong việc giải bài tập, để dễ tính toán, người ta thường lấy hoặc đôi khi lấy .
Đơn vị tính:
a/Định nghĩa:
Vận tốc trung bình là thương số giữa độ dời (độ dịch chuyển) vật di chuyển được và thời gian di chuyển hết độ đời đó.
b/Công thức
Chú thích:
: vận tốc trung bình của vật (m/s).
: độ dời của vật (m).
: độ dịch chuyển của vật (m)
: thời gian chuyển động của vật (s).
: tọa độ của vật ở vị trí 1 và 2 (m)
: thời điểm 1 và 2 trong chuyển động của vật (s)
Lưu ý
+ Vận tốc trung bình có thể âm hoặc dương tùy theo cách chọn chiều dương. Khi chọn chiều dương cùng chiều chuyển động vận tốc trung bình mang giá trị dương. Ngược lại, khi chọn chiều dương ngược chiều chuyển động vận tốc trung bình mang giá trị âm.
+ Vận tốc trung bình qua hai tọa độ có độ lớn giống nhau trong mọi hệ quy chiếu.
+ Một vật đi A đến B rồi từ B về A thì vận tốc trung bình trên cả quá trình bằng không dù đi trên đoạn đường với vận tốc khác nhau. Lúc này vận tốc trung bình không thể hiện được mức độ nhanh chậm của chuyển động.
1.Chuyển động thẳng đều
a/Định nghĩa : Chuyển động thẳng đều là chuyển động của vật có chiều và vận tốc không đổi , quỹ đạo có dạng đường thẳng.
Ví dụ: chuyển động của vật trên băng chuyền, đoàn duyệt binh trong những ngày lễ lớn.

Quân đội Nga duyệt binh kỉ niệm ngày chiến thắng 9/5
2.Phương trình chuyển đông thẳng đều
a/Công thức :
b/Chứng minh :
Chọn chiều dương là chiều chuyển động , gốc thời gian là lúc xuất phát
Vật xuất phát tại vị trí x ,quãng đường đi được sau t:
Mặc khác độ dời của vật :

Hình ảnh minh họa cho công thức
Vật chuyển động thẳng đều theo chiều dương nên
tính từ lúc bắt đầu chuyển động
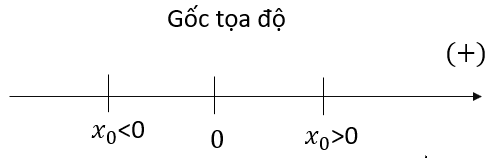
Chú thích:
: Tọa độ của vật tại thời điểm t (m).
: Tọa độ ban đầu của vật ở thời điểm t=0s.
: Vận tốc của vật (m/s).
: Cùng hướng chuyển động.
: Ngược hướng chuyển động.
: Thời gian chuyển động của vật (s).
Quãng đường
a/Định nghĩa
Quãng đường S là tổng độ dịch chuyển mà vật đã thực hiện được mang giá trị dương.
Trong chuyển động thẳng đều, quãng đường mang tính tích lũy, nó có thể khác với độ dời . Ví dụ, khi vật đi theo chiều âm tọa độ của vật giảm dần dẫn tới độ dời mang giá trị âm để tìm quãng đường ta lấy trị tuyệt đối của độ dời.
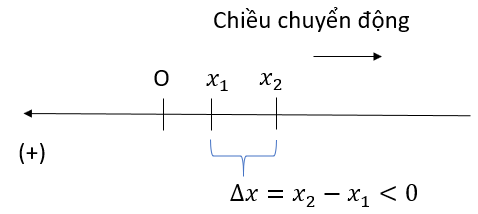
Đối với vật chuyển động thẳng theo chiều dương đã chọn thì quãng đường chính là độ dời.
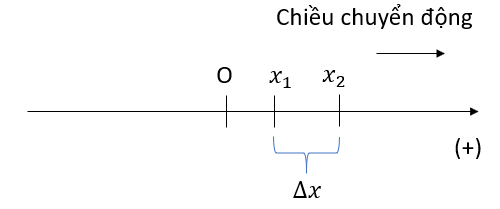
Trong thực tế khi làm bài tập, người ta thường chọn (vật xuất phát ngay tại gốc tọa độ). Chiều dương là chiều chuyển động nên thường có (quãng đường đi được bằng đúng tọa độ lúc sau của vật).
b/Công thức:
Chú thích:
: là quãng đường (m).
: là tọa độ của vật ở thời điểm đầu và sau (m).
v: vận tốc của chuyển động (m/s)
: thời gian chuyển động (s)
c/Lưu ý:
Trong trường hợp xe đi nhiều quãng đường nhỏ với tốc độ khác nhau. Thì quãng đường mà xe đã chuyển động được chính là bằng tổng những quãng đường nhỏ đó cộng lại với nhau.
a/Định nghĩa
Gia tốc được tính bằng tỉ số giữa độ biến thiên vận tốc của vật và thời gian diễn ra. Nó là một đại lượng vectơ. Một vật có gia tốc chỉ khi tốc độ của nó thay đổi (chạy nhanh dần hay chậm dần) hoặc hướng chuyển động của nó bị thay đổi (thường gặp trong chuyển động tròn).
+Ý nghĩa : Đặc trưng cho sự biến đổi vận tốc nhiều hay ít của chuyển động.
b/Công thức
Chú thích:
: vận tốc lúc sau của vật
: vận tốc lúc đầu của vật
: thời gian chuyển động của vật
: gia tốc của vật
Đặc điểm
Nếu vật chuyển động theo chiều dương của trục tọa độ thì.
+ Chuyển động nhanh dần a>0.
+ Chuyển động chậm dần a<0.
Và ngược lại,nếu chuyển đông theo chiều âm của trục tọa độ.
+ Chuyển động nhanh dần a<0.
+ Chuyển động chậm dần a>0.
Nói cách khác:
Nếu gia tốc cùng chiều vận tốc () thì vật chuyển động nhanh dần đều.
Nếu gia tốc ngược chiều vận tốc () thì vật chuyển động chậm dần đều.
Chú thích:
: tọa độ lúc đầu của vật - tại thời điểm xuất phát .
: tọa độ lúc sau của vật - tại thời điểm t đang xét .
: vận tốc của vật ở thời điểm .
: gia tốc của vật .
: thời gian chuyển động của vật .
hay
Chú thích:
: quãng đường (m).
: vận tốc lúc đầu của vật .
: thời gian chuyển động của vật .
: gia tốc của vật
Ứng dụng:
Xác định vận tốc của vật ở một thời điểm xác định.
Chú thích:
: vận tốc của vật tại thời điểm đang xét .
: vận tốc của vật tại thời điểm ban đầu .
: gia tốc của vật .
: thời gian chuyển động .
Đặc điểm :Chuyển động rơi tự do là chuyển động thẳng , nhanh dần đều với gia tốc trong trường g và có vận tốc đầu bằng 0.
Chứng minh
Từ công thức quãng đường của nhanh dần đều.
Suy ra trong chuyển động rơi tự do quãng đường có công thức
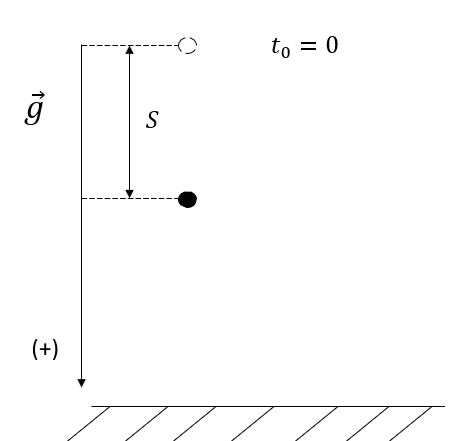
Chú thích:
: Quãng đường vật rơi từ lúc thả đến thời điểm t .
g: Gia tốc trọng trường . Tùy thuộc vào vị trí được chọn mà g sẽ có giá trị cụ thể.
: thời gian chuyển động của vật từ lúc thả
Chú thích:
: thời gian chuyển động của vật .
: độ cao của vật so với mặt đất .
: gia tốc trọng trường . Tùy thuộc vào vị trí được chọn mà g sẽ có giá trị cụ thể.
Chú thích:
: tốc độ của vật .
g: gia tốc trọng trường . Tùy thuộc vào vị trí được chọn mà g sẽ có giá trị cụ thể.
: thời điểm của vật tính từ lúc thả
Lưu ý:
Ở đây ta chỉ tính tới độ lớn của vận tốc tức thời của vật (nói cách khác là ta đang tính tốc độ tức thời của vật).
Chu kì
a/Định nghĩa : Chu kì của vật trong chuyển động tròn đều là thời gian để vật quay hết một vòng.
Ví dụ : Chu kì của Trái Đất quay xung quanh Mặt trời là 365 ngày.
+ Ý nghĩa : Sau khoảng thời gian T , vật sẽ có cùng trạng thái đó .Thể hiện tính tuần hoàn của chuyển động tròn đều.
b/Công thức:
Chú thích:
: chu kì .
: tần số .
: tốc độ góc .
: số chuyển động tròn thực hiện được .
t: thời gian thực hiện hết số dao động đó .
Chú thích:
: vận tốc ban đầu của vật, trong trường hợp này là vận tốc ném .
: độ cao của vật .
: thời gian chuyển động của vật .
: gia tốc trọng trường do trái đất tác động lên vật .
: tầm xa cực đại của vật .
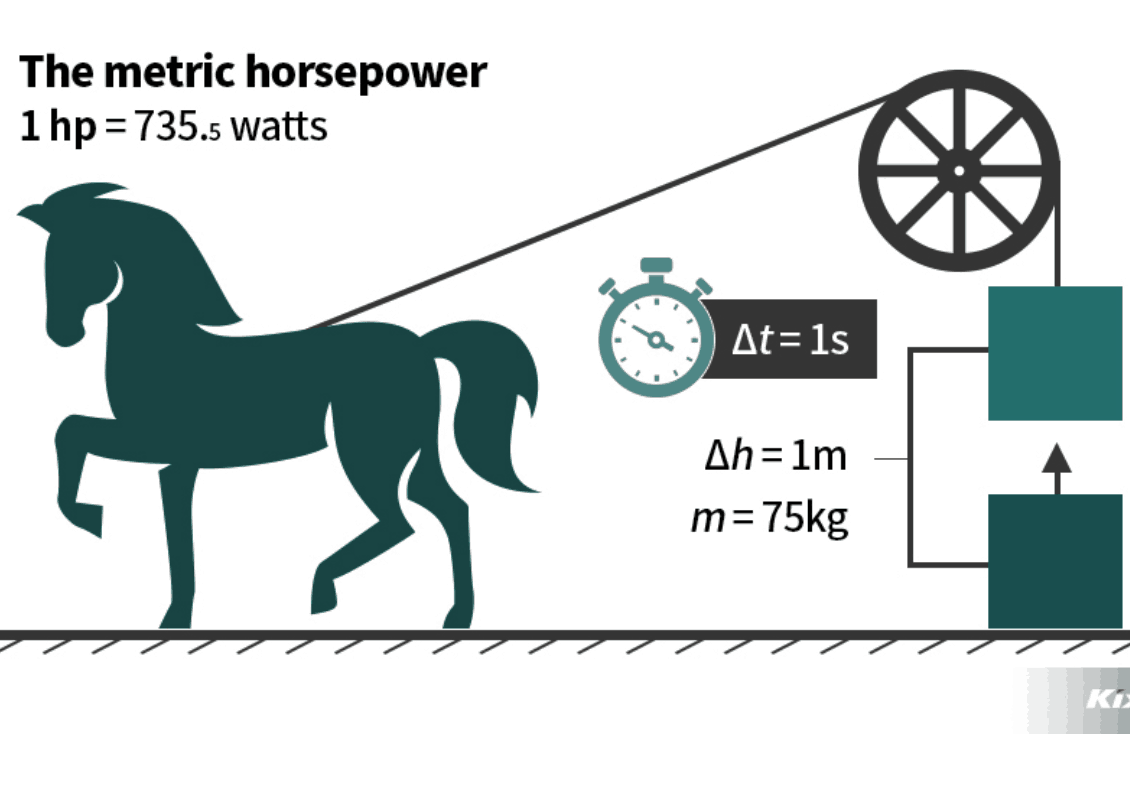
Định nghĩa:
Công suất là đại lượng đo bằng công sinh ra trong một đơn vị thời gian.
Chú thích:
: công cơ học .
: thời gian thực hiện công đó .
: công suất .
Khái niệm: Dòng điện không đổi (dòng điện một chiều) là dòng điện có chiều và cường độ không thay đổi theo thời gian.
Viết tắt: 1C hay DC.
Chú thích:
: cường độ dòng điện
: điện lượng chuyển qua tiết diện thẳng của vật dẫn
: thời gian
Ứng dụng:
Khi cúp điện chúng ta thường dùng đèn pin dạng sạc hoặc đèn pin sử dụng pin tiểu để chiếu sáng. Đây cũng chính là nguồn sử dụng pin 1 chiều phổ biến nhất.

Điện thoại di động chúng ta thường dùng hàng ngày cũng chính là một thiết bị dùng điện một chiều bởi vì nó được cắm sạc trực tiếp từ nguồn điện xoay chiều. Đầu cắm sạc chính là đầu chuyển nguồn AC (xoay chiều) thành DC (một chiều) trước khi vào điện thoại.

Một ứng dụng đang được sử dụng rộng rãi và càng ngày càng nhân rộng chính là tấm Pin thu năng lượng mặt trời để biến thành điện năng sử dụng. Quá trình nãy cũng cần phải có thiết bị biến tần để biến điện năng một chiều thành điện xoay chiều 220VAC để sử dụng.

Ngoài ra acquy và pin cũng là những nguồn điện cho ra dòng điện một chiều.


Phát biểu: Lượng điện năng mà một đoạn mạch tiêu thụ khi có dòng điện chạy qua để chuyển hóa thành các dạng năng lượng khác được đo bằng công của lực điện thực hiện khi dịch chuyển có hướng các điện tích.
Chú thích:
: điện năng tiêu thụ của đoạn mạch (
: hiệu điện thế
: độ lớn của điện tích
: cường độ dòng điện
: thời gian
Vận dụng: Điện năng tiêu thụ thông thường được đo bằng đồng hồ điện, hay còn gọi là công tơ điện.
Đơn vị đo: 1 = 3600000 = 3600000

Phát biểu: Công suất điện của một đoạn mạch là công suất tiêu thụ điện năng của đoạn mạch đó và có trị số bằng điện năng mà đoạn mạch tiêu thụ trong một đơn vị thời gian, hoặc bằng tích của hiệu điện thế giữa hai đầu đoạn mạch và cường độ dòng điện chạy qua đoạn mạch đó.
Chú thích:
: công suất điện của đoạn mạch
: điện năng tiêu thụ
: thời gian
: hiệu điện thế giữa hai đầu đoạn mạch
: cường độ dòng điện
Dụng cụ dùng để đo công suất thường dùng là Watt kế.

Phát biểu: Nhiệt lượng tỏa ra ở một vật dẫn tỉ lệ thuận với điện trở của vật dẫn, với bình phương cường độ dòng điện và với thời gian dòng điện chạy qua vật dẫn đó.
Chú thích:
: nhiệt lượng tỏa ra ở đoạn mạch
: điện trở của đoạn mạch
: cường độ dòng điện
: thời gian
Trong đó điện trở được tính bằng công thức: .
: điện trở
: điện trở suất
: chiều dài vật dẫn
: tiết diện ngang của vật dẫn

Heinrich Lenz (1804 - 1865)

James Prescott Joule (1818 - 1889)
Phát biểu: Công suất tỏa nhiệt ở vật dẫn khi có dòng điện chạy qua đặc trưng cho tốc độ tỏa nhiệt của vật dẫn đó và được xác định bằng nhiệt lượng tỏa ra ở vật dẫn trong một đơn vị thời gian.
Chú thích:
: công suất tỏa nhiệt
: nhiệt lượng tỏa ra của dây dẫn
: thời gian
: điện trở của vật dẫn
: cường độ dòng điện
Phát biểu: Công của nguồn điện bằng điện năng tiêu thụ trong toàn mạch.
Chú thích:
: công của nguồn điện
: suất điện động của nguồn điện
: điện lượng
: cường độ dòng điện
: thời gian (s)
Phát biểu: Công suất của nguồn điện đặc trưng cho tốc độ thực hiện công của nguồn điện đó và được xác định bằng công của nguồn điện thực hiện trong một đơn vị thời gian. Công suất này cũng chính bằng công suất tiêu thụ điện năng của toàn mạch.
Chú thích:
: công suất của nguồn điện
: công của nguồn điện
: thời gian
: suất điện động của nguồn
: cường độ dòng điện
Hiện tượng điện phân
a/Định nghĩa hiện tượng điện phân:
Hiện tượng điện phân là hiện tượng xuất hiện các phản ứng phụ ở các điện cực khi cho dòng điện một chiều qua bình điện phân.
b/Công thức Faraday về chất điện phân
Chú thích:
: khối lượng của chất được giải phóng ra ở điện cực khi điện phân
: số Faraday
: khối lượng mol nguyên tử của nguyên tố
: hóa trị của nguyên tố
: cường độ dòng điện trong dung dịch điện phân
: thời gian điện phân
c/Ứng dụng:
Hiện tượng điện phân có nhiều ứng dụng trong thực tế sản xuất và đời sống như luyện kim, tinh luyện đồng, điều chế clo, xút, mạ điện, đúc điện,...
1. Luyện nhôm
Bể điện phân có cực dương là quặng nhôm nóng chảy, cực âm bằng than, chất điện phân là muối nhôm nóng chảy, dòng điện vào khoảng 10000A.

2. Mạ điện
Bể điện phân có cực dương là một tấm kim loại để mạ, cực âm là vật cần mạ, chất điện phân thường là dung dịch muối kim loại để mạ. Dòng điện được chọn một cách thích hợp để đảm bảo chất lượng của lớp mạ.
Michael Faraday (1791 - 1867)

Định nghĩa: Hình chiếu của một vật chuyển động tròn đều lên đường kính của nó là một dao động đều hòa.
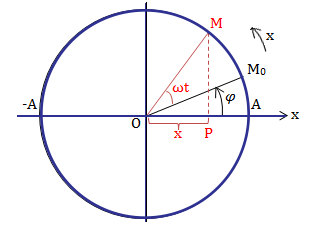
Chú thích:
: Li độ của chất điểm tại thời điểm .
Thời gian .
: Biên độ dao động ( li độ cực đại) của chất điểm .
: Tần số góc (tốc độ góc) .
: Pha dao động tại thời điểm .
: Pha ban đầu của dao động tại thời điểm .
Đồ thị:
Đồ thị của tọa độ theo thời gian là đường hình sin.
Khái niệm:
Vận tốc là đạo hàm của li độ theo thời gian:
Chú thích:
v: Vận tốc của chất điểm tại thời điểm
: Biên độ dao động (li độ cực đại) của chất điểm
: Tần số góc ( tốc độ góc)
: Pha dao động tại thời điểm
: Pha ban đầu của chất điểm tại thời điểm
Thời gian
Đồ thị:
Đồ thị vận tốc theo thời gian là đường hình sin.
Đồ thị vận tốc theo li độ là hình elip.
Liên hệ pha:
Vận tốc sớm pha so với li độ Li độ chậm (trễ) pha so với vận tốc.
Gia tốc sớm pha so với vận tốc Vận tốc chậm (trễ) pha so với gia tốc.
Gia tốc là đạo hàm của vận tốc theo thời gian.
.
Chú thích:
: Gia tốc của chất điểm tại thời điểm
: Biên độ dao động (li độ cực đại) của chất điểm
: Tần số góc (tốc độ góc)
: Pha dao động tại thời điểm
: Pha ban đầu của chất điểm tại thời điểm
Thời gian
Liên hệ pha:
Gia tốc sớm pha so với vận tốc Vận tốc chậm (trễ) pha so với gia tốc.
Gia tốc sớm pha so với li độ ( ngược pha ).
Đồ thị:
Đồ thị gia tốc theo thời gian là đường hình sin.
Đồ thị gia tốc theo li độ là một đường thẳng.
Đồ thị gia tốc theo vận tốc là một elip.
Khái niệm:
Chu kỳ của dao động điều hòa là khoảng thời gian để vật thực hiện một dao động toàn phần.
Chú thích:
: Chu kỳ dao động .
: Tần số góc (tốc độ góc) .
: Số dao động mà chất điểm thực hiện được trong khoảng thời gian .
Thời gian thực hiện hết số dao động .
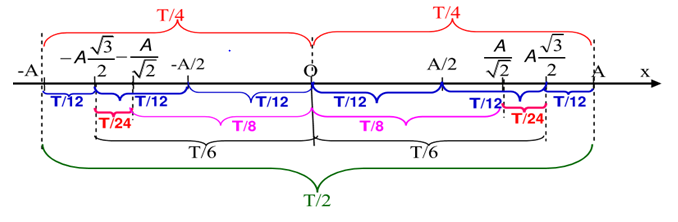
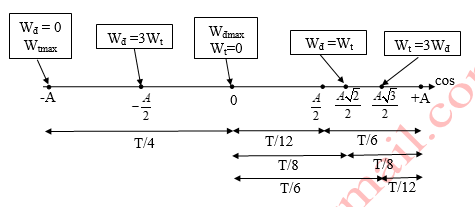
Lưu ý:
Thời gian vật đi được tại các vị trí đặc biệt:
Khái niệm:
Tần số của dao động điều hòa là số dao động chất điểm thực hiện được trong một giây.
Chú thích:
: Tần số dao động .
: Tần số góc (tốc độ góc) .
: Chu kỳ dao động của vật .
: Số dao động mà chất điểm thực hiện được trong khoảng thời gian .
Thời gian thực hiện hết số dao động .
Khái niệm:
Tốc độ của một vật là độ lớn của sự thay đổi vị trí của nó.
Chú thích:
: tốc độ trung bình của chất điểm
: Quãng đường mà chất điểm đi được trong thời gian
: Thời gian vật chuyển động
Lưu ý:
+ Tốc độ trung bình của chất điểm chuyển động trong một chu kỳ :
.
+ Tốc độ trung bình của chất điểm chuyển động trong nửa chu kỳ:
Khái niệm:
Vận tốc trung bình trong khoảng thời gian nhất định được định nghĩa là tỉ số giữa sự thay đổi vị trí trong khoảng thời gian đang xét và khoảng thời gian đó.
Chú thích:
: Vận tốc trung bình của chất điểm
: Độ dời của chất điểm
: Vị trí của vật tại thời điểm bắt đầu xét chuyển động
: Vị trí của vật sau khi chuyển động trong thời gian
: Thời gian chuyển động của vật
Nguyên tắc: Vật đi được quãng đường dài nhất khi li độ điểm đầu và điểm cuối có giá trị đối nhau.
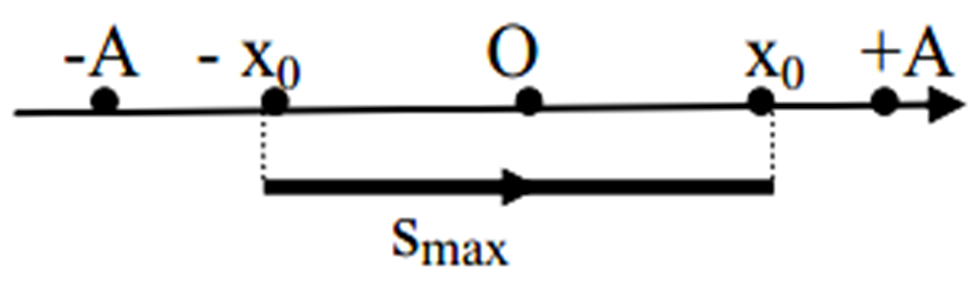
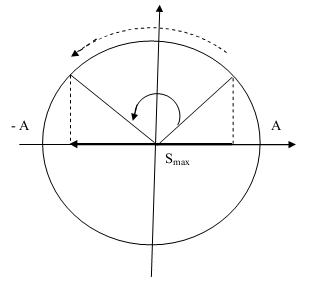
Chú thích:
: Quãng đường lớn nhất chất điểm chuyển động trong khoảng thời gian
: Biên độ dao động
: góc quét của chất điểm trong khoảng thời gian
Với: và
Lưu ý:
+ Nếu khoảng thời gian thì tách:. Với :.
+ Công thức còn có thể viết :
Với: .
Nguyên tắc: Vật đi được quãng đường ngắn nhất khi li độ điểm đầu và điểm cuối có giá trị bằng nhau.
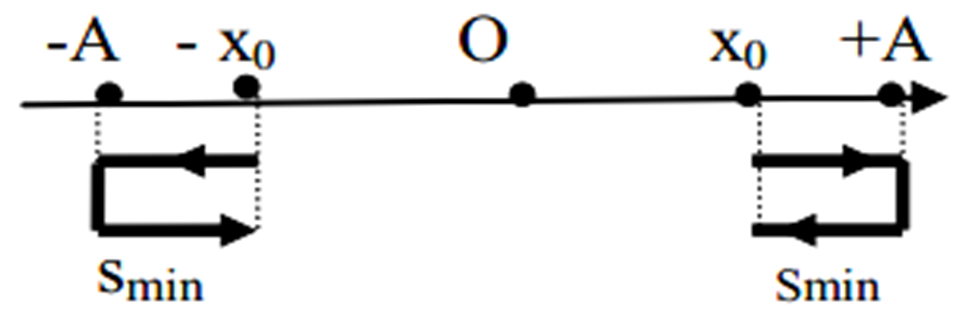
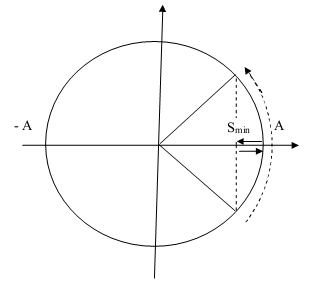
Chú thích:
: Quãng đường nhỏ nhất chất điểm chuyển động trong khoảng thời gian
: Biên độ dao động
: góc quét của chất điểm trong khoảng thời gian
Với: và
Lưu ý:
+ Nếu khoảng thời gian thì tách:. Với :.
+ Công thức còn có thể viết :
Với: .
Khái niệm:
Tốc độ trung bình là thương số giữa quãng đường chất điểm đi được và thời gian để đi hết được quãng đường đó. Đây cũng là khái niệm mà chúng ta đã được học ở chương trình lớp 10.
Chú thích:
: Tốc độ trung bình của chất điểm
: Quãng đường chất điểm đi được
: Thời gian mà vật chuyển động được quãng đường
Lưu ý:
+ Tốc độ trung bình của chất điểm trong một chu kỳ: .
+Tốc độ trung bình của chất điểm trong nửa chu kỳ:
Chú thích:
: Tốc độ trung bình của chất điểm
: Quãng đường lớn nhất chất điểm đi được trong khoảng thời gian
: Thời gian chuyển động của chất điểm
Lưu ý:
với
Chú thích:
: Tốc độ trung bình của chất điểm
: Quãng đường nhỏ nhất chất điểm đi được trong khoảng thời gian
: Thời gian chuyển động của chất điểm
Lưu ý:
với
Khái niệm:
Chu kỳ của lắc lò xo dao động điều hòa là khoảng thời gian vật thực hiện được một dao động toàn phần.
Chú thích:
: Chu kỳ dao động .
: Tần số góc (tốc độ góc) .
: Số dao động mà chất điểm thực hiện được trong khoảng thời gian .
Thời gian thực hiện hết số dao động .
: Khối lượng vật treo trên lò xo .
: Độ cứng của lò xo .
: Gia tốc trọng trường .
: Độ biến dạng của lò xo tại vị trí cân bằng .
Lưu ý:
Ta có :
Khái niệm:
Tần số dao động là số dao động và chất điểm thực hiện được trong một giây.
Chú thích:
: Tần số dao động .
: Tần số góc (tốc độ góc) .
: Chu kỳ dao động của vật .
: Số dao động mà chất điểm thực hiện được trong khoảng thời gian .
Thời gian thực hiện hết số dao động .
Định nghĩa : năng lượng mà lò xo có được dưới dạng chuyển động.Động năng biến thiên điều hòa theo t với chu kì
Công thức :
Chú ý : Động năng cực đại ở VTCB, cực tiểu ở biên.
Chú thích:
Động năng của lò xo .
Khối lượng của vật .
Vận tốc của vật .
Biên độ dao động cùa lò xo
Độ cứng của lò xo .
Li độ của vật
Định nghĩa : năng lượng mà lò xo có được khi bị biến dạng đàn hồi.Thế năng biến thiên điều hòa theo t với chu kì
Công thức :
Chú ý : Thế năng cực tiểu ở VTCB, cực đại ở biên.
Chú thích:
Thế năng của lò xo .
Khối lượng của vật .
Vận tốc của vật .
Biên độ dao động cùa lò xo
Độ cứng của lò xo .
Pha ban đầu của dao động
Li độ của vật
Ta lấy tỉ số :
Với n là số tự nhiên dương ví dụ : 1,3,5,6,7,8,14,...
m là số bán nguyên ví dụ : 0,5 ; 1,5
q là phần dư nhỏ hơn 0,5
Quãng đường vật đi :
Tính s :
+
+
Khi hướng về biên
Khi ;
Khi ;
Khi hướng về vị trí cân bằng:
Công thức :
Với : tần số quay của thanh .
: tốc độ góc .
N: số vòng
t : thời gian
Khi :đồng hồ chạy chậm lại.
Khi : đồng hồ chạy nhanh lên
Thời gian chạy nhanh hay chậm trong t:
Với : Thời gian đồng hồ chạy nhanh hay chậm trong t
Thời gian
Độ biến thiên chu kì
Chu kì con lắc chạy đúng
Khi nhiệt độ thay đổi từ đến :
Công thức
Với là hệ số nở dài
Khoảng thời gian nhanh, chậm :
Trong 1 chu kì
Số lần vật đi theo chiều âm hoặc chiều dương: 1
Số lần vật đổi chiều trong 1 chu kì : 2
Số lần vật có cùng giá trị : 2
Số lần vật có cùng độ lớn : 4
Số lần vật đi theo chiều âm hoặc chiều dương: 1
Công thức xác định số lần thỏa điều kiện trong khoảng thời gian :
Khi không lấy chiều
:
Tính = ,với góc quét là từ vị trí trí đang xét đến vị trí tiếp
số lần
khi lấy chiều
Thời gian ngắn nhất để vật thỏa yêu cầu bài toán
Bước 1 : Xác định vị trí ban đầu xét.
Bước 2 : Xác định vị trí lần đầu vật thỏa yêu cầu bài toán
Bước 3 : Tính góc quay suy ra , Với là góc quay
Hoặc dùng VTLG:
Trong 1 chu kì
Số lần vật đi theo chiều âm hoặc chiều dương: 1
Số lần vật đổi chiều trong 1 chu kì : 2
Số lần vật có cùng giá trị : 2
Số lần vật có cùng độ lớn : 4
Số lần vật đi theo chiều âm hoặc chiều dương: 1
Công thức xác định số lần thỏa điều kiện giá trị trong khoảng thời gian :
Không xét chiều
:
Tính = ,với góc quét là từ vị trí trí đang xét đến vị trí tiếp
số lần
Khi ta lấy thêm chiều :
Những thời điểm vật có gia tốc , lực phục hồi thỏa điều kiện
và
Thời gian bay trong tụ :
Hạt chuyển động ném ngang :
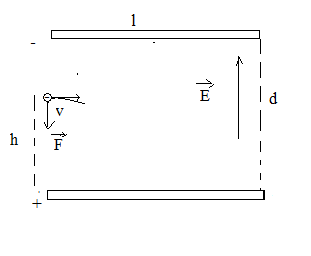
Thời gian chuyển động theo phương ngang trong khoảng chiều dài tụ :
Thời gian bay đến bản dương :
Thời gian bay trong bản tụ là
s : quãng đường e đi được
U: độ lớn hiệu điện thế dăt vào bản tụ
d: khoảng cách giữa hai bản tụ
s : quãng đường e đi được
U: độ lớn hiệu điện thế dăt vào bản tụ
d: khoảng cách giữa hai bản tụ
Với số photon phát ra
công suất nguồn chiếu sáng
L: Nhiệt hóa hơi
: Nhiệt dung riêng
D: Khối lượng riêng của nước
Với V: thể tích vật bị nóng chảy
Nhiệt nóng chảy
t thời gian thu và phát sóng
S quãng đường sóng đi được
c vận tốc ánh sáng
Chu kì sóng
Thời gian
: số lần nhấp nhô hoặc số đỉnh sóng tới
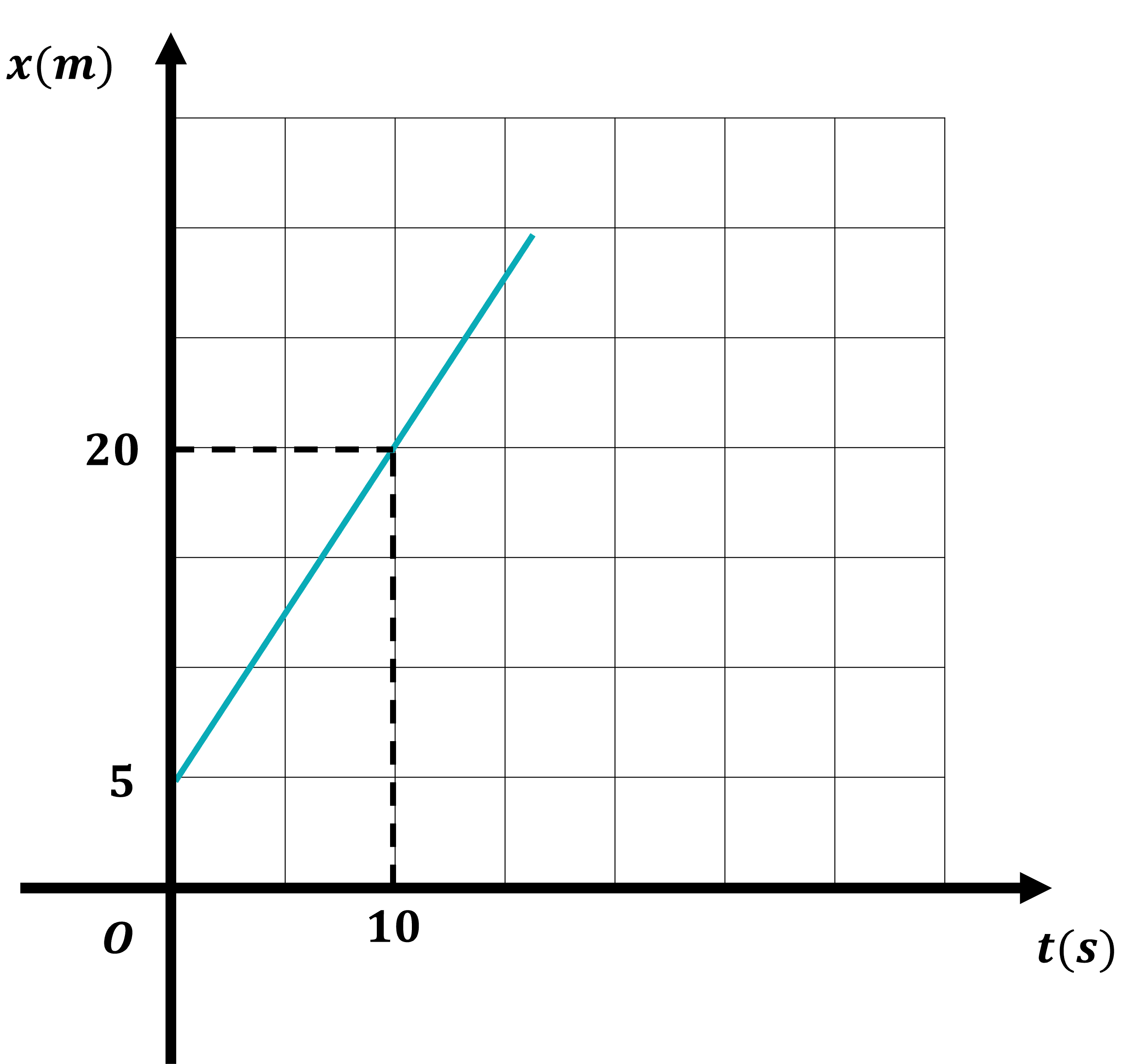
Đồ thị chuyển động thẳng đều trong hệ tọa độ (xOt) là đường thẳng.
Trục tung Ox : thể hiện vị trí của vật.
Vị trí ban đầu : Vị trí của điểm đầu tiên trên đồ thị của đường thẳng của chuyển động hạ vuông góc với Ox,
Trục hoành Ot: thể hiện thời gian.
Thời điểm bắt đầu xét : Thời điểm này có được bằng cách lấy điểm đầu tiên trên đồ thị của chuyển động hệ vuông góc với Ot.
(1) Vật đang đứng yên
(2) Vật chuyển động thẳng đều ngược chiều dương đã chọn.
(3) Vật chuyển động thẳng đều cùng chiều dương đã chọn.
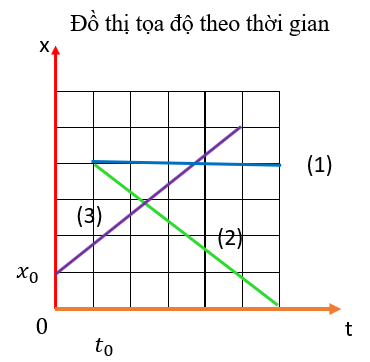
tọa độ tại thời điểm đầu.
thời điểm bắt đầu xét chuyển động.
Lấy một điểm trên đồ thị đoạn thẳng hạ vuông góc lên các trục ta tìm được tọa độ và thời điểm tương ứng.
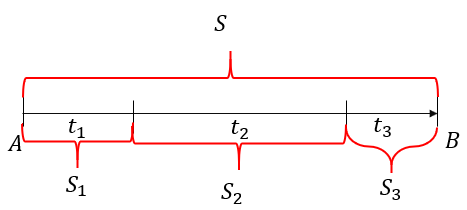
Với S là quãng đường từ A đến B.
thời gian trên từng quãng đường.
1.Thời gian, thời điểm, gốc thời gian:
a/Gốc thời gian : Thời điểm người ta bắt đầu xét có giá trị bằng không.
Ví dụ : Gốc thời gian có thể chọn là lúc bắt đầu chuyển động ; trước và sau chuyển động một khoảng thời gian.
Gốc thời gian có thể chọn theo thời gian thực (thời gian hằng ngày):
Ví dụ : Tàu khởi hành lúc 19h00 : thời gian điểm khởi hành là 19h00 gốc thời gian lúc này là 0h00 .Gỉa sử bạn ở nơi tàu lúc này và đang 18h00 thì thời điểm khởi hành là 1h00 gốc thời gian lúc này là 18h00.

b/ Thời điểm: Giá trị thời gian so với gốc thời gian
thời điểm = khoảng thời gian gốc thời gian
Ví dụ : Xét khoảng thời gian từ 0h đến 5h : ta chọn gốc thời gian là 0 h thì trên đồng hồ chỉ thời điểm 5-0=5 h. Còn khi ta chọn gốc thời gian là 2 h thì trên đồng hồ chỉ thời điểm 5-2=3 h.Đối với chọn gốc thời gian trước 0h00 ví dụ như 21h00 trước đó , thì thời điểm 5h lúc này trở thành thời điểm 3+5=8h theo gốc thời gian mới.
c/ Khoảng thời gian là hiệu của hai thời điểm.Có giá trị lớn hơn không và không phụ thuộc vào việc chọn gốc thời gian.
Lưu ý : cần phân biệt rõ hai khái niệm thời điểm và khoảng thời gian.
2. Gốc tọa độ, tọa độ:
a/Gốc tọa độ : Vị trí có tọa độ bằng không.
b/Tọa độ của vật : giá trị của hình chiếu của vật lên các trục tọa độ.
Trong hệ tọa độ một chiều
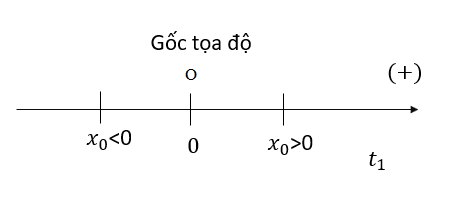
+ Vật nằm về phía chiều dương mang giá trị dương.
+ Vật nằm về phía chiều âm mang giá trị âm.
3.Hệ quy chiếu là thuật ngữ để chỉ vật mốc và hệ tọa độ gắn với vật mốc dùng để xác định vị trí của vật chuyển động cùng với gốc thời gian và đồng hồ để đo thời gian.
1. Rơi tự do
a/Định nghĩa : Rơi tự do là sự rơi của vật chỉ tác dụng của trọng lực và vận tốc đầu bằng không.
b/Đặc điểm:
+ Phương : thẳng đứng
+ Chiều : hướng xuống.
+ Nhanh dần đều với gia tốc g.Gia tốc g khác nhau ở các nơi trên Trái Đất
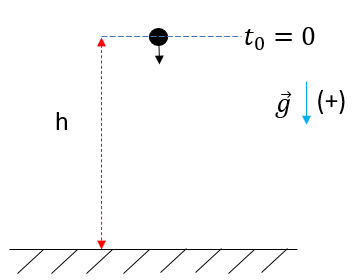
2. Phương trình rơi rự do:
a/Công thức
Với là độ cao lúc thả rơi.Chiều dương cùng chiều chuyển động.
+ Ý nghĩa : Trong thực nghiệm dùng để tính gia tốc rơi tự do nơi làm thí nghiệm.
b/Chứng minh:
+ Vật chuyển động nhanh dần đều từ 0 đến t:
+ Độ cao vật lúc này :
Nhận xét : thời gian trôi qua càng nhiều thì độ cao của vật càng giảm.
Xét bài toán hai xe chuyển động từ A đến B. Hai xe cùng xuất phát tại A, để hai xe gặp nhau thì một xe có vận tốc lớn hơn và xuất phát chậm hơn một khoảng thời gian a với xe còn lại.
Chọn chiều dương từ A đến B, gốc tọa độ tại A, gốc thời gian lúc xe 2 bắt đầu chuyển động.
Phương trình xe 1 :
Phương trình xe 2 :
Vị trí gặp nhau :
Thời điểm gặp nhau từ lúc xe 1 chuyển động
Xét bài toán hai xe chuyển động cùng chiều từ A đến B .Xe 1 xuất phát tại A , xe 2 xuất phát tại vị trí cách A một đoạn b. Hai xuất phát cùng lúc.
Chọn gốc tọa độ tại A, gốc thời gian là lúc bắt đầu, chiều dương là chiều chuyển động.
Phương trình chuyển động xe 1 : .
Phương trình chuyển động xe 2:
Vị trí hai xe gặp nhau
Nhận xét : Vận tốc của xe có tọa độ ban đầu lớn hơn sẽ có vận tốc nhỏ hơn dễ hai xe gặp nhau.
Xét bài toán hai xe chuyển động trên AB: xe 1 bắt đầu từ A ,xe 2 bắt đầu từ C (cách A một đoạn d ) hướng về A .Hai xe xuất phát cùng lúc
Chọn chiều dương là chiều chuyển động của xe 1 , gốc tọa độ tại A, gốc thời gian là lúc xuất phát.
Phương trình chuyển động xe 1 :
Phương trình chuyển động xe 2:
Vị trí hai xe gặp nhau :
Đồ thị vận tốc trong hệ tọa độ (vOt) có dạng đường thẳng.
Đồ thị gia tốc trong hệ tọa độ (aOt) có dạng đường thẳng vuông góc trục gia tốc.
Đồ thị tọa độ trong hệ tọa độ (xOt) có dạng parabol.
Ta chỉ xét phần đồ thị nét liền
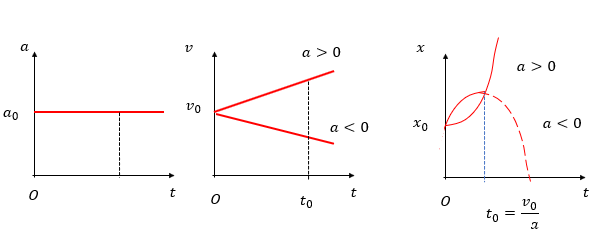
Với chiều dương ban đầu cùng chiều chuyển động :
Trong hệ tọa độ (vOt)
Vật chuyển động chậm dần với gia tốc , vận tốc đầu có phương trình chuyển động :
Vì vật chuyển động một chiều :
Xét bài toán hai xe chuyển động trên AB: xe 1 bắt đầu từ A, xe 2 bắt đầu từ C (cách A một đoạn d ) hướng về A. Xe 1 xuất phát sớm hơn xe 2 một khoảng thời gian là a.
Chọn chiều dương là chiều chuyển động của xe 1 , gốc tọa độ tại A, gốc thời gian là lúc xe 1 xuất phát.
Phương trình chuyển động xe 1 :
Phương trình chuyển động xe 2:
Vị trí hai xe gặp nhau :
Khi thả viên đá rơi xuống giếng (hoặc hang động). Viên đá sẽ rơi tự do xuống giếng sau đó va đập vào đáy giếng và tạp ra âm thanh truyền lên miệng giếng. Ta có hệ phương trình sau:
Thế (1) vào (2) Từ đây ta có
Chú thích:
: thời gian từ lúc thả rơi viên đá đến khi nghe được âm thanh vọng lên .
thời gian viên đá rơi tự do từ miệng giếng xuống đáy giếng .
: thời gian tiếng đọng di chuyển từ dưới đáy lên miệng giếng .
: vận tốc truyền âm trong không khí .
: gia tốc trọng trường
: độ sâu của giếng hoặc hang động
Vận tốc tức thời là vận tốc tại một thời điểm xác định, được kí hiệu là .
Một chất điểm dao động điều hòa trên trục Ox theo phương trình trong đó x tính bằng (cm) và t tính bằng (s). Tại thời điểm t = 5s vận tốc của chất điểm là bao nhiêu?
Một vật dao động điều hòa với . Và vận tốc có độ lớn cực đại là . Xác định chu kì dao động của vật.
Một vật nhỏ dao động điều hòa theo phương trình trong đó x tính bằng cm và t tính bằng giây. Phase ban đầu của chất điểm là?
Một chất điểm dao động điều hòa với phương trình (cm). Hỏi biên độ của chất điểm là bao nhiêu?
Một chất điểm dao động điều hòa với phương trình (cm) trong đó x tính bằng cm và t tính bằng giây. Hỏi tần số góc của chất điểm là bao nhiêu?
Một con lắc lò xo đang dao động điều hòa theo phương ngang. Nếu A tăng gấp 2 lần thì tần số dao động sẽ
Một chất điểm thực hiện dao động điều hòa với chu kì và biên độ . Tại thời điểm chất điểm đi qua vị trí cân bằng thì vận tốc của nó có độ lớn bằng
Một vật dao động điều hoà xung quanh vị trí cân bằng với biên độ dao động là A và chu kì T. Tại điểm có li độ x = A/2 tốc độ của vật là
Một chất điểm M chuyển động đều trên một đường tròn với tốc độ dài 160cm/s và tốc độ góc 4 rad/s. Hình chiếu P của chất điểm M trên một đường thẳng cố định nằm trong mặt phẳng hình tròn dao động điều hòa với biên độ và chu kì lần lượt là
Một vật dao động điều hoà, trong thời gian 1 phút vật thực hiện được 30 dao động. Chu kì dao động của vật là?
Một vật dao động điều hoà có phương trình dao động là (cm). Vận tốc của vật khi có li độ x = 3cm là
Một vật dao động điều hoà có phương trình dao động là (cm). Lấy . Gia tốc của vật khi có li độ x = 3cm là bao nhiêu?
Một vật dao động điều hòa trên đoạn thẳng dài 10cm và thực hiện được 50 dao động trong thời gian 78,5 giây. Tìm vận tốc và gia tốc của vật khi đi qua vị trí có li độ x = -3cm theo chiều hướng về vị trí cân bằng.
Một vật dao động điều hòa khi vật có li độ x1 = 3cm thì vận tốc của vật là v1 = 40cm/s, khi vật qua vị trí cân bằng thì vận tốc của vật là v2 = 50cm/s. Tần số của dao động điều hòa là.
Một vật dao động điều hòa trên quỹ đạo dài 40cm. Khi vật ở vị trí x = 10cm thì vật có vận tốc là . Chu kì dao động của vật là
Một vật dao động điều hòa dọc theo trục Ox. Vận tốc của vật khi qua vị trí cân bằng là 62,8cm/s và gia tốc ở vị trí biên là 2m/s2. Lấy . Biên độ và chu kì dao động của vật lần lượt là
Vận tốc của một vật dao động điều hoà khi đi qua vị trí cân bằng là 1cm/s và gia tốc của vật khi ở vị trí biên là . Chu kì dao động của vật là?
Phương trình dao động của một vật dao động điều hoà có dạng (cm). Li độ của vật khi pha dao động bằng là bao nhiêu?
Phương trình vận tốc của một vật dao động điều hoà là v = 120cos20t(cm/s), với t đo bằng giây. Vào thời điểm t = T/6(T là chu kì dao động), vật có li độ là
Đối với dao động tuần hoàn, khoảng thời gian ngắn nhất mà sau đó trạng thái dao động của vật được lặp lại như cũ được gọi là?
Trong phương trình dao động điều hoà , các đại lượng là những đại lượng trung gian cho phép xác định
Chọn phát biểu sai khi nói về dao động điều hòa
Trong dao động điều hòa, gia tốc biến đổi như thế nào?
Chọn phát biểu đúng. Biên độ dao động của con lắc lò xo không ảnh hưởng đến
Gọi T là chu kì dao động của một vật dao động tuần hoàn. Tại thời điểm t và tại thời điểm (t + nT) với n là số nguyên thì vật ra sao?
Đại lượng nào sau đây tăng gấp đôi khi tăng gấp đôi biên độ dao động điều hòa của con lắc lò xo
Trong các phương trình sau phương trình nào không biểu thị cho dao động điều hòa ?
Phương trình dao động của một vật có dạng . Chọn kết luận đúng.
Phương trình dao động của vật có dạng . Pha ban đầu của dao động là
Trong chuyển động dao động điều hoà của một vật thì tập hợp ba đại lượng nào sau đây là không thay đổi theo thời gian?
Phương trình dao động cơ điều hoà của một chất điểm là . Gia tốc của nó sẽ biến thiên điều hoà với phương trình:
Một vật dao động điều hoà với phương trình (cm). Biết ở thời điểm t có li độ là 3cm. Li độ dao động ở thời điểm sau đó 1/10(s) là
Một vật dao động điều hoà với phương trình (cm). Biết ở thời điểm t có li độ là 3cm. Li độ dao động ở thời điểm sau đó là?
Một vật dao động điều hoà với phương trình (cm). Thời điểm đầu tiên vật có vận tốc bằng nửa độ lớn vận tốc cực đại là
Một vật dao động điều hoà với phương trình . Biết ở thời điểm t có li độ là -8cm. Li độ dao động ở thời điểm sau đó 13s là
Một vật dao động điều hoà khi đi qua vị trí cân bằng có tốc độ bằng 6m/s và gia tốc khi vật ở vị trí biên bằng 18m/s2. Tần số dao động của vật bằng
Phương trình biểu diễn dao động điều hoà của một chất điểm. Gốc thời gian đã được chọn khi?
Chu kì của dao động điều hòa là gì? Chọn phát biểu đúng.
Phase ban đầu của dao động điều hòa phụ thuộc?
Một vật dao động điều hòa theo phương trình . Nếu tại một thời điểm nào đó vật đang có li độ x = 3cm và đang chuyển động theo chiều dương thì sau đó 0,25 s vật có li độ là?
Vật dao động điều hòa khi?
Vật dao động điều hòa khi đi từ biên độ dương về vị trí cân bằng thì.
Khi vật dao động điều hòa, đại lượng không thay đổi là
Trong dao động điều hoà, gia tốc biến đổi như thế nào?
Một vật dao động điều hòa trên trục Ox, xung quanh vị trí cân bằng là gốc tọa độ. Gia tốc của vật phụ thuộc vào li độ x theo phương trình: . Số dao động toàn phần vật thực hiện được trong mỗi giây là?
Vật dao động điều hoà có gia tốc biến đổi theo phương trình Ở thời điểm ban đầu ( t = 0 s) vật ở ly độ?
Vật dao động điều hoà theo hàm cosin với biên độ 4 cm và chu kỳ 0,5 s ( lấy ) .Tại một thời điểm mà pha dao động bằng thì vật đang chuyển động lại gần vị trí cân bằng .Gia tốc của vật tại thời điểm đó là?
Gia tốc tức thời trong dao động điều hoà biến đổi:
Một chất điểm dao động điều hoà theo phương trình phase dao động của chất điểm ở thời điểm t = 1s là?
Phát biểu nào sau đây về sự so sánh li độ, vận tôc và gia tốc là đúng? Trong dao động điều hòa, li độ, vận tốc và gia tốc là ba đại lượng biến đổi điều hòa theo thời gian và có
Phát biểu nào sau đây về mối quan hệ giữa li độ, vận tốc, gia tốc là đúng?
Một chất điểm có khối lượng m dao động điều hoà xung quanh vị cân bằng với biên độ A. Gọi vmax , amax, Wđmax lần lượt là độ lớn vận tốc cực đại, gia tốc cực đại và động năng cực đại của chất điểm. Tại thời điểm t chất điểm có ly độ x và vận tốc là v. Công thức nào sau đây là không dùng để tính chu kì dao động điều hoà của chất điểm ?
Trong dao động điều hoà, gia tốc luôn luôn
Một con lắc lò xo treo thẳng đứng, độ dài tự nhiên của lò xo là 22cm. Vật mắc vào lò xo có khối lượng m = 120g. Khi hệ thống ở trạng thái cân bằng thì độ dài của lò xo là 24cm. Lấy . Tần số dao động của vật là
Một chất điểm dao động điều hoà dọc trục Ox quanh VTCB O với biên độ A và chu kì T. Trong khoảng thời gian T/4 quãng đường lớn nhất mà chất điểm có thể đi được là
Một chất điểm dao động điều hoà dọc trục Ox quanh VTCB O với biên độ A và chu kì T. Trong khoảng thời gian T/3 quãng đường lớn nhất mà chất điểm có thể đi được là
Một chất điểm dao động điều hoà dọc trục Ox quanh VTCB O với biên độ A và chu kì T. Trong khoảng thời gian quãng đường lớn nhất mà chất điểm có thể đi được là
Một vật dao động điều hoà theo phương trình (cm). Quãng đường vật đi được trong thời gian t = 0,125s là
Một chất điểm dao động dọc theo trục Ox. Phương trình dao động là (cm). Sau thời gian t = 0,5s kể từ khi bắt đầu chuyển động quãng đường S vật đã đi được là :
Một chất điểm dao động dọc theo trục Ox. Phương trình dao động là (cm). Trong thời gian t = 0,157 s kể từ khi bắt đầu chuyển động, quãng đường S vật đã đi là
Cho một vật dao động điều hoà với phương trình (cm). Tìm quãng đường vật đi được kể từ lúc t = 0 đến lúc t = 2,5s.
Một vật dao động điều hoà theo phương trình (cm). Quãng đường vật đi được sau thời gian 2,4s kể từ thời điểm ban đầu bằng :
Một vật dao động điều hoà có phương trình . Quãng đường mà vật đi được sau thời gian 12,125s kể từ thời điểm ban đầu bằng :
Một con lắc gồm một lò xo có độ cứng k = 100N/m, khối lượng không đáng kể và một vật nhỏ khối lượng 250g, dao động điều hoà với biên độ bằng 10cm. Lấy gốc thời gian t = 0 là lúc vật đi qua vị trí cân bằng. Quãng đường vật đi được trong đầu tiên là
Vật dao động điều hòa theo phương trình : (cm). Quãng đường vật đi trong 0,05 s là :
Vật dao động điều hòa theo phương trình: . Quãng đường vật đi trong s (kể từ t = 0) là :
Một vật dao động điều hoà có phương trình dao động: trong đó x tính bằng cm và t tính bằng giây. Quãng đường vật đi được sau 0,375s tính từ thời điểm ban đầu bằng bao nhiêu?
Một vật đang dao động điều hòa với vận tốc cực đại là 31,4 cm/s. Lấy π = 3,14. Tốc độ trung bình trong 1 chu kỳ dao động là bao nhiêu?
Một vật đang dao động điều hòa với chu kỳ T. Trong thời gian ngắn nhất khi đi từ vị trí x = A đến x = tốc độ trung bình của chất điểm là bao nhiêu?
Một vật dao động điều hòa trên một quỹ đạo thẳng dài 14cm, T = 1s. Tính từ thời điểm vật qua vị trí có li độ x = 3,5 cm theo chiều dương đến khi gia tốc của vật đạt giá trị cực tiểu lần thứ 2, vật có tốc độ trung bình là?
Một chất điểm dao động dọc theo trục Ox. Phương trình dao động là x = 4cos4 t(cm). Vận tốc trung bình của chất điểm trong 1/2 chu kì là, chọn t=0 khi chất điểm xuất phát tại vị trí biên dương.
Một vật dao động điều hoà với tần số f = 2Hz. Tốc độ trung bình của vật trong thời gian nửa chu kì là?
Một vật dao động điều hoà theo phương trình x = 4 cos ( 8)(cm) . Tốc độ trung bình của vật khi đi từ vị trí có li độ x1 = cm theo chiều dương đến vị trí có li độ x2 = cm theo chiều dương bằng :
Một vật dao động điều hoà theo phương trình x = 5cos (2 )(cm). Tốc độ trung bình của vật trong một chu kì dao động bằng:
Một vật dao động điều hoà với chu kì T = 0,4s và trong khoảng thời gian đó vật đi được quãng đường 16cm. Tốc độ trung bình của vật khi đi từ vị trí có li độ đến vị trí có li độ cm theo chiều dương là
Vật dao động điều hòa theo phương trình : x = 4cos(20 t - ) cm. Tốc độ trung bình của vật sau khi đi quãng đường S = 2 cm ( kể từ t = 0) là?
Một chất điểm dao động điều hòa trên trục Ox với biên độ 10 cm, chu kì 2 s. Mốc thế năng ở vị trí cân bằng. Tốc độ trung bình của chất điểm trong khoảng thời gian ngắn nhất khi chất điểm đi từ vị trí có động năng bằng 3 lần thế năng đến vị trí có động năng bằng 1/3 lần thế năng là:
Một chất điểm dao động điều hòa xung quanh vị trí cân bằng với biên độ 5 cm, tần số 5 Hz. Vận tốc trung bình của chất điểm khi nó đi từ vị trí biên dương qua vị trí cân bằng đến vị trí biên âm là :
Một vật dao động điều hòa với phương trình dao động trong đó x tính bằng cm và t tính bằng giây. Từ thời điểm t = 0, khoảng thời gian ngắn nhất để gia tốc của vật có độ lớn bằng phân nửa gia tốc cực đại là
Một vật dao động điều hoà theo phương trình x = 10cos()(cm). Thời điểm vật đi qua vị trí N có li độ = 5cm lần thứ 2009 theo chiều dương là
Một vật dao động điều hoà theo phương trình x = 10cos()(cm). Thời điểm vật đi qua vị trí N có li độ = 5cm lần thứ 1000 theo chiều âm là
Một vật dao động điều hoà theo phương trình x = 10cos()(cm). Thời điểm vật đi qua vị trí N có li độ = 5cm lần thứ 2008 là
Một chất điểm dao động dọc theo trục Ox. Theo phương trình dao động x = 2cos() (cm). Thời gian ngắn nhất vật đi từ lúc bắt đầu dao động đến lúc vật có li độ x = cm là
Một chất điểm dao động với phương trình dao động là. Thời gian ngắn nhất vật đi từ lúc bắt đầu dao động đến lúc vật có li độ là
Một chất điểm dao động dọc theo trục Ox. Phương trình dao động là x = 4cos(5t)(cm). Thời gian ngắn nhất vật đi từ lúc bắt đầu dao động đến lúc vật đi được quãng đường S = 6cm là
Một vật dao động điều hoà với tần số bằng 5Hz. Thời gian ngắn nhất để vật đi từ vị trí có li độ bằng - 0,5A(A là biến độ dao động) đến vị trí có li độ bằng +0,5A là
Một vật dao động điều hoà với phương trình x = Acos(). Biết trong khoảng thời gian 1/30s đầu tiên, vật đi từ vị trí = 0 đến vị trí x = theo chiều dương. Chu kì dao động của vật là
Một vật dao động điều hoà theo phương trình . Thời gian ngắn nhất để vật đi từ vị trí có li độ = 2cm đến li độ = 4cm bằng
Một chất điểm dao động điều hoà với phương trình x = 4cos(2πt + π/2)cm. Thời gian từ lúc bắt đầu dao động đến lúc đi qua vị trí x = 2cm theo chiều dương của trục toạ độ lần thứ 1 là
Một vật dao động điều hoà quanh vị trí cân bằng theo phương trình x = 4cos() (cm) ; t tính bằng giây . Biết rằng cứ sau những khoảng thời gian /40 (s) thì động năng lại bằng nửa cơ năng . Tại những thời điểm nào thì vật có vận tốc bằng không ?
Một vật đang dao động điều hòa với chu kỳ T biên độ 5cm. Trong một chu kì thời gian để vật nhỏ của lò xo có độ lớn gia tốc không vượt quá 100 là . Lấy = 10. Tần số dao động của vật là bao nhiêu?
Một vật dao động điều hòa với chu kì T. Gọi là tốc độ trung bình của chất điểm trong một chu kì dao động, v là vận tốc tức thời của chất điểm. Trong một chu kì dao động, khoảng thời gian mà ≥ là?
Một vật dao động theo phương trình , trong đó x được tính bằng cm và t được đo bằng giây. Trong giây đầu tiên vật đi qua vị trí N có mấy lần?
Một chất điểm dao động điều hoà có vận tốc bằng không tại hai thời điểm liên tiếp là và . Tính từ thời điểm ban đầu ( ) đến thời điểm chất điểm đã đi qua vị trí cân bằng
Cho dao động điều hoà có phương trình dao động: (cm) trong đó, t đo bằng s. Sau 8/3s tính từ thời điểm ban đầu, vật qua vị trí có li độ x = -1cm bao nhiêu lần ?
Một vật dao động điều hoà với tần số góc = 5rad/s. Lúc t = 0, vật đi qua vị trí có li độ x = -2cm và có tốc độ 10(cm/s) hướng về phía vị trí biên gần nhất. Phương trình dao động của vật là
Một vật chuyển động theo phương trình (x có đơn vị cm; t có đơn vị giây). Hãy tìm câu trả lời đúng?
Một chất điểm dao động điều hoà với tần số f = 5Hz. Khi phase dao động bằng rad thì li độ của chất điểm là cm, phương trình dao động của chất điểm biết ban đầu chất điểm ở biên dương là:
Một chất điểm dao động với phương trình x=10cos(2πt) (cm). Quãng đường chất điểm đi được trong 1 chu kỳ dao động là?
Vật dao động điều hoà theo phương trình . Thời gian vật đi được quãng đường kể từ thời điểm ban đầu là?
Một vật dao động điều hoà theo phương trình . Quãng đường vật đi được trong thời gian t = 0,05s là?
Một vật dao động điều hoà theo phương trình (cm). Kể từ lúc t = 0, quãng đường vật đi được sau 5s bằng
Một vật dao động điều hoà theo phương trình (cm). Kể từ lúc t = 0, quãng đường vật đi được sau 12,375s bằng
Một vật dao động điều hoà có phương trình x = 8cos(7πt + π/6)cm. Khoảng thời gian tối thiểu để vật đi từ vị trí có li độ cm đến vị trí có li độ cm là
Một chất điểm dao động điều hoà dọc trục Ox quanh VTCB O với biên độ A và chu kì T. Theo phương trình với x tính bằng cm và t tính bằng s. Hãy xác định quãng đường nhỏ nhất vật đi được trong t = 1/6 (s)
Một vật dao động điều hoà với chu kỳ T và biên độ A. Tốc độ trung bình lớn nhất của vật thực hiện được trong khoảng thời gian là
Một vật dao động điều hoà với chu kỳ T và biên độ A. Tốc độ trung bình nhỏ nhất của vật thực hiện được trong khoảng thời gian là
Một vật dao động điều hoà xung quanh vị trí cân bằng theo phương trình .Biết rằng cứ sau những khoảng thời gian bằng thì động năng của vật lại bằng thế năng. Chu kì dao động của vật là:
Năng lượng của một vật dao động điều hoà là E. Khi li độ bằng một nửa biên độ thì động năng của nó bằng.
Một vật dao động điều hoà, cứ sau một khoảng thời gian 2,5s thì động năng lại bằng thế năng. Tần số dao động của vật là
Một vật dao động điều hoà, khi vật có li độ thì vận tốc ; khi vật có li độ thì vận tốc . Động năng và thế năng biến thiên với chu kỳ
Phát biểu nào sau đây về động năng và thế năng trong dao động điều hòa là không đúng ?
Phát biểu nào sau đây về động năng và thế năng trong dao động điều hòa là không đúng ?
Khi con lắc dao động với phương trình thì thế năng của nó biến đổi với tần số :
Phát biểu nào sau đây về động năng và thế năng trong dao động điều hoà là không đúng?
Con lắc lò xo dao động điều hòa với tần số 5 Hz, thế năng của con lắc sẽ biến thiên với tần số
Một vật dao động điều hoà theo thời gian có phương trình thì động năng và thế năng cũng dao động tuần hoàn với tần số góc
Con lắc lò xo dao động điều hòa với tần số f. Động năng và thế năng của con lắc biến thiên tuần hoàn với tần số là
Động năng của một vật dao động điều hoà : . Giá trị lớn nhất của thế năng là
Phương trình dao động cơ điều hoà của một chất điểm, khối lượng m, là . Động năng của nó biến thiên theo thời gian theo phương trình:
Kết luận nào sau đây không đúng? Đối với một chất điểm dao động cơ điều hoà với tần số f thì
Cho một con lắc lò xo dao động điều hoà với phương trình (cm). Biết vật nặng có khối lượng m = 100g. Động năng của vật nặng tại li độ x = 8cm bằng
một con lắc lò xo dao động điều hoà với phương trình (cm). Biết vật nặng có khối lượng m = 100g. Thế năng của con lắc tại thời điểm t = (s) bằng
Một con lắc lò xo có vật nặng khối lượng m = 1kg dao động điều hoà trên phương ngang. Khi vật có vận tốc v = 10cm/s thì thế năng bằng ba lần động năng. Năng lượng dao động của vật là
Con lắc lò xo có vật nặng khối lượng m = 100g, chiều dài tự nhiên 20cm treo thẳng đứng. Khi vật cân bằng lò xo có chiều dài 22,5cm. Kích thích để con lắc dao động theo phương thẳng đứng. Thế năng của vật khi lò xo có chiều dài 24,5cm là
Một vật nặng 500g dao động điều hoà trên quỹ đạo dài 20cm và trong khoảng thời gian 3 phút vật thực hiện 540 dao động. Cho . Cơ năng của vật khi dao động là
Một con lắc lò xo dao động theo phương thẳng đứng. Trong thời gian 1 phút, vật thực hiện được 50 dao động toàn phần giữa hai vị trí mà khoảng cách 2 vị trí này là 12cm. Cho g = 10m/; lấy = 10. Xác định độ biến dạng của lò xo khi hệ thống ở trạng thái cân bằng
Một vật dao động điều hoà với phương trình thì động năng và thế năng của nó cũng biến thiên tuần hoàn với tần số
Một vật dao động điều hoà với biên độ 4cm, cứ sau một khoảng thời gian 1/4 giây thì động năng lại bằng thế năng. Quãng đường lớn nhất mà vật đi được trong khoảng thời gian 1/6 giây là
Một lò xo có chiều dài tự nhiên = 20cm, độ cứng k = 20N/m. Gắn lò xo trên thanh nhẹ OA nằm ngang, một đầu lò xo gắn với O, đầu còn lại gắn quả cầu có khối lượng m = 200g, quả cầu chuyển động không ma sát trên thanh ngang. Cho thanh quay tròn đều trên mặt phẳng ngang thì chiều dài lò xo là 25cm. Trong 1 giây thanh OA quay được số vòng là
Một lò xo nhẹ có độ dài tự nhiên 20cm, giãn ra thêm 1 cm nếu chịu lực kéo 0,1N. Treo vào lò xo 1 hòn bi có khối lượng 10g quay đều xung quanh trục thẳng đứng () với tốc độ góc . Khi ấy, lò xo làm với phương thẳng đứng góc . Lấy g = Số vòng vật quay trong 1 phút là
Một lò xo nhẹ có độ dài tự nhiên 20cm, giãn ra thêm 1cm nếu chịu lực kéo 0,1N. Treo một hòn bi nặng m = 10g vào lò xo rồi quay đều lò xo xung quanh một trục thẳng đứng () với vận tốc góc . Khi ấy, trục lò xo làm với phương thẳng đứng góc . Lấy g = . Số vòng quay trong 2 phút bằng
Con lắc lò xo nằm ngang. Khi vật đang đứng yên ở vị trí cân bằng ta truyền cho vật nặng vận tốc v = 31,4cm/s theo phương ngang để vật dao động điều hoà. Biết biên độ dao động là 5cm, chu kì dao động của con lắc là :
Một lò xo dãn thêm 2,5cm khi treo vật nặng vào. Lấy g = = 10m/. Chu kì dao động tự do của con lắc bằng :
Một lò xo nếu chịu tác dụng lực kéo 1N thì giãn ra thêm 1cm. Treo một vật nặng 1kg vào lò xo rồi cho nó dao động thẳng đứng. Chu kì dao động của vật là :
Con lắc lò xo treo thẳng đứng dao động điều hoà, thời gian vật nặng đi từ vị trí cao nhất đến vị trí thấp nhất là 0,2s. Tần số dao động của con lắc là :
Kích thích để con lắc lò xo dao động điều hoà theo phương ngang với biên độ 5cm thì vật dao động với tần số 5Hz. Treo hệ lò xo trên theo phương thẳng đứng rồi kích thích để con lắc lò xo dao động điều hoà với biên độ 3cm thì tần số dao động của vật là :
Khi treo một vật có khối lượng m = 81g vào một lò xo thẳng đứng thì tần số dao động điều hoà là 10Hz. Treo thêm vào lò xo vật có khối lượng m’ = 19g thì tần số dao động của hệ là :
Một con lắc lò xo treo thẳng đứng dao động với biên độ 4cm, chu kì 0,5s. Khối lượng quả nặng 400g. Lấy 10, cho g = 10m/. Độ cứng của lò xo là :
Vật có khối lượng m = 200g gắn vào lò xo. Con lắc này dao động với tần số f = 10Hz. Lấy = 10. Độ cứng của lò xo bằng :
Một lò xo treo phương thẳng đứng, khi mắc vật m1 vào lò xo thì hệ dao động với chu kì = 1,2s. Khi mắc vật m2 vào lò xo thì vật dao động với chu kỳ = 0,4 s. Biết = 180g. Khối lượng vật là :
Một vật khối lượng 1kg treo trên một lò xo nhẹ có tần số dao động riêng 2Hz. Treo thêm một vật thì thấy tần số dao động riêng bằng 1Hz. Khối lượng vật được treo thêm bằng :
Một lò xo có độ cứng k = 25N/m. Lần lượt treo hai quả cầu có khối lượng , vào lò xo và kích thích cho dao động thì thấy rằng. Trong cùng một khoảng thời gian: thực hiện được 16 dao động, thực hiện được 9 dao động. Nếu treo đồng thời 2 quả cầu vào lò xo thì chu kì dao động của chúng là T = (s). Khối lượng của hai vật lần lượt bằng :
Một lò xo có độ cứng k. Lần lượt treo vào lò xo hai vật có khối lượng . Kích thích cho chúng dao động, chu kì tương ứng là 1s và 2s. Biết khối lượng của chúng hơn kém nhau 300g. Khối lượng hai vật lần lượt bằng
Một chất điểm dao động điều hòa có đồ thị như hình vẽ. Phương trình vận tốc là
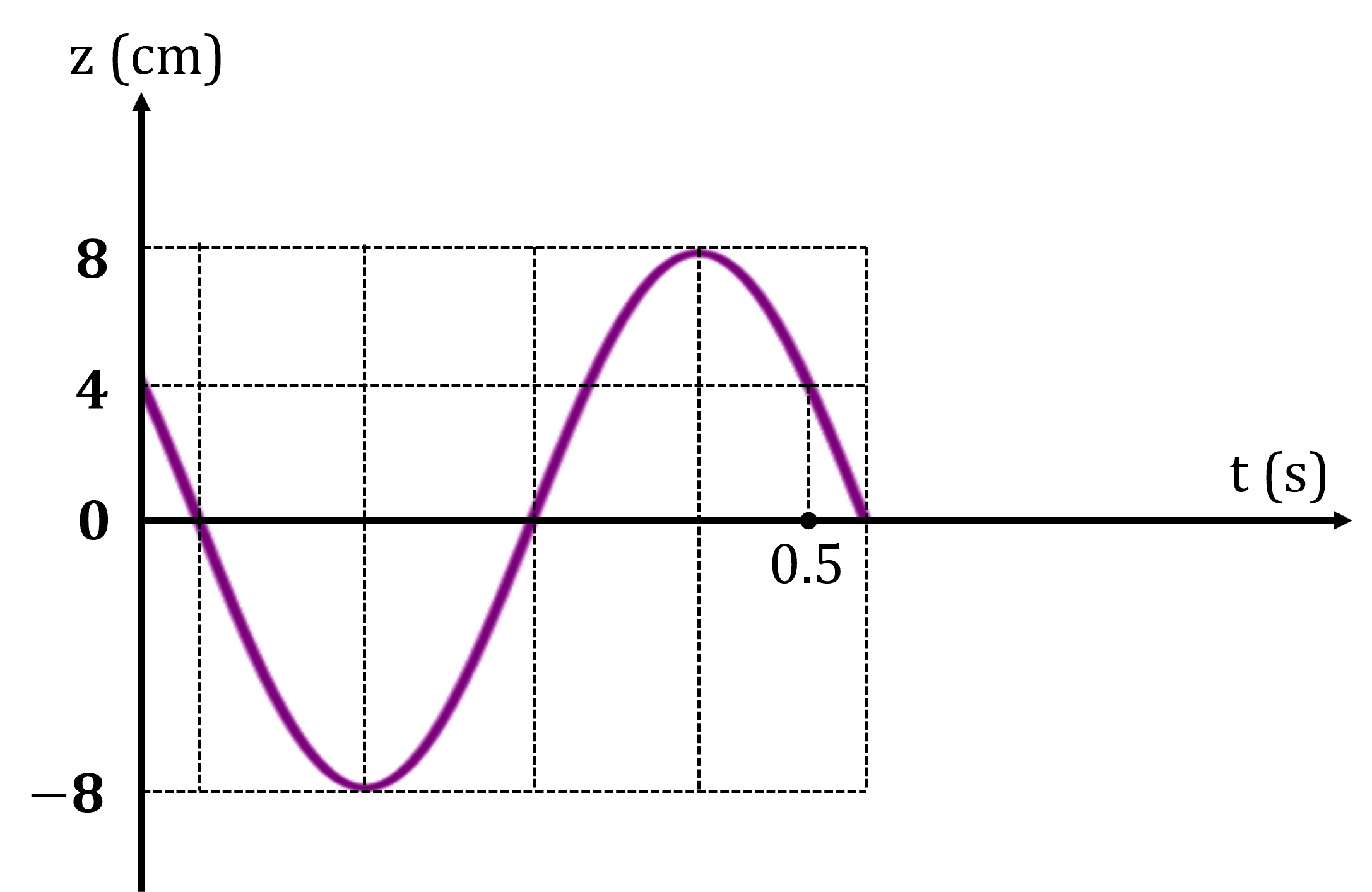
Một con lắc lò xo gồm một lò xo có độ cứng k = 100N/m và vật có khối lượng m = 250g, dao động điều hoà với biên độ A = 6cm. Chọn gốc thời gian t = 0 lúc vật qua vị trí cân bằng. Quãng đường vật đi được trong (s) đầu tiên là
Một vật nhỏ, khối lượng m, được treo vào đầu một lò xo nhẹ ở nơi có gia tốc rơi tự do bằng 9,8m/. Khi vật ở vị trí cân bằng lò xo giãn ra một đoạn bằng 5,0 cm. Kích thích để vật dao động điều hoà. Thời gian ngắn nhất để vật đi từ vị trí cân bằng đến vị trí có li độ bằng nửa biên độ là
Một vật nhỏ, khối lượng m, được treo vào đầu một lò xo nhẹ ở nơi có gia tốc rơi tự do bằng 9,8m/. Khi vật ở vị trí cân bằng lò xo giãn ra một đoạn bằng 5,0cm. Kích thích để vật dao động điều hoà. Thời gian ngắn nhất để vật đi từ vị trí có vận tốc cực đại đến vị trí có động năng bằng 3 lần thế năng là
Cho g = 10m/. Ở vị trí cân bằng lò xo treo theo phương thẳng đứng giãn 10cm, thời gian vật nặng đi từ lúc lò xo có chiều dài cực đại đến lúc vật qua vị trí cân bằng lần thứ hai là:
Một con lắc lò xo dao động theo phương thẳng đứng với phương trình (cm). (chiều dương hướng xuống; gốc O tại vị trí cân bằng). Lấy g = 10m/. Cho biết khối lượng của vật là m = 1 kg. Tính thời gian ngắn nhất từ lúc t = 0 đến lúc lực đàn hồi cực đại lần thứ nhất bằng
Cho một con lắc lò xo treo thẳng đứng. Khi treo vật m vào lò xo giãn 5cm. Biết vật dao động điều hoà với phương trình: x =10cos()(cm). Chọn trục toạ độ thẳng đứng, gốc O tại vị trí cân bằng, chiều dương hướng xuống. Thời gian ngắn nhất kể từ lúc t = 0 đến lúc lực đẩy đàn hồi cực đại lần thứ nhất bằng
Một con lắc lò xo treo thẳng đứng dao động điều hoà với biên độ 4cm, chu kì 0,5s. Khối lượng quả nặng 400g. Lấy g =10m/. Giá trị cực đại của lực đàn hồi tác dụng vào quả nặng là
Con lắc lò treo thẳng đứng, lò xo có khối lượng không đáng kể. Hòn bi đang ở vị trí cân bằng thì được kéo xuống dưới theo phương thẳng đứng một đoạn 3cm rồi thả cho dao động. Hòn bi thực hiện 50 dao động mất 20s. Lấy g = 10m/. Tỉ số độ lớn lực đàn hồi cực đại và lực đàn hồi cực tiểu của lò xo khi dao động là
Cho một con lắc lò xo dao động điều hoà theo phương thẳng đứng, biết rằng trong quá trình dao động có /= 7/3. Biên độ dao động của vật bằng 10cm. Lấy g = 10m/ = m/. Tần số dao động của vật bằng
Một con lắc lò xo treo thẳng đứng, lò xo có độ cứng 100N/m. Ở vị trí cân bằng lò xo giãn 4cm. Truyền cho vật động năng 0,125J vật dao động theo phương thẳng đứng. g = 10m/, . Chu kì và biên độ dao động của vật là
Con lắc lò xo nằm ngang có k =100 N/m, m = 1kg dao động điều hoà. Khi vật có động năng 10mJ thì cách VTCB 1cm, khi có động năng 5mJ thì cách VTCB là
Khi treo vật nặng có khối lượng m vào lò xo có độ cứng thì vật dao động với chu kì . Khi treo vật nặng đó vào lò xo có độ cứng thì vật dao động điều hoà với chu kì là
Một vật có khối lượng treo vào lò xo có độ cứng là k thì dao động với tần số là 5 Hz. Khi treo vật nặng có khối lượng vào lò xo đó thì vật dao động với tần số là
Khi treo vật có khối lượng m vào một lò xo có độ cứng là k thì vật dao động với tần số 10Hz, nếu treo thêm gia trọng có khối lượng 60g thì hệ dao động với tần số 5Hz. Khối lượng m bằng
Cho hai lò xo giống nhau có cùng độ cứng là k, lò xo thứ nhất treo vật = 400g dao động với , lò xo thứ hai treo dao động với chu kì . Trong cùng một khoảng thời gian con lắc thứ nhất thực hiện được 5 dao động, con lắc thứ hai thực hiện được 10 dao động. Khối lượng m2 bằng
Khi gắn quả cầu vào lò xo thì nó dao động với chu kì = 0,4s. Khi gắn quả cầu vào lò xo đó thì nó dao động với chu kì = 0,9s. Khi gắn quả cầu = vào lò xo thì chu kì dao động của con lắc là
Một con lắc lò xo treo vào trần thang máy. Khi thang máy đứng yên con lắc dao động với chu kì T. Khi thang máy chuyển động thẳng nhanh dần đều đi lên thẳng đứng thì con lắc dao động với chu kì T' bằng
Con lắc lò xo, đầu trên cố định, đầu dưới gắn vật có khối lượng m dao động điều hòa theo phương thẳng đứng ở nơi có gia tốc trọng trường g. Khi vật ở vị trí cân bằng, độ giãn của lò xo là Δl. Chu kỳ dao động của con lắc được tính bằng biểu thức :
Trong dao động điều hoà của con lắc lò xo, nếu khối lượng của vật nặng tăng thêm 44% so với khối lượng ban đầu thì số dao động toàn phần vật thực hiện được trong mỗi giây so với ban đầu sẽ
Chu kì dao động con lắc lò xo tăng 2 lần khi
Mắc vật có khối lượng với hệ lò xo , mắc song song thì chu kì dao động của hệ là . Nếu 2 lò xo này mắc nối tiếp nhau thì chu kì dao động là (s) ; biết . Độ cứng lần lượt là :
Cho một lò xo có chiều dài OA = = 50cm, độ cứng = 20N/m. Treo lò xo OA thẳng đứng, O cố định. Móc quả nặng m = 1kg vào điểm C của lò xo. Cho quả nặng dao động theo phương thẳng đứng. Biết chu kì dao động của con lắc là 0,628s. Điểm C cách điểm treo O một khoảng bằng
Một người đi từ Hà Nội lúc 9:00 am đến lúc 11:00 am cùng ngày thì về đến Hải Phòng.
Tàu Thống nhất Bắc Nam xuất phát từ ga Hà Nội vào lúc tới ga Vinh vào lúc 0h30 phút ngày hôm sau.
Một chất điểm dao động điều hoà dọc trục Ox quanh VTCB O với biên độ A và chu kì T. Theo phương trình với x tính bằng cm và t tính bằng s. Hãy xác định quãng đường nhỏ nhất vật đi được trong t = 1/3 (s).
Một chất điểm dao động điều hoà dọc trục Ox quanh VTCB O với biên độ A và chu kì T. Theo phương trình với x tính bằng cm và t tính bằng s. Hãy xác định quãng đường nhỏ nhất vật đi được trong t = 1/8 (s)
Múi giờ tại Hà Nội sớm hơn Moscow 4 giờ. Thời gian bay từ Hà Nội đi Moscow là 9h35m.
Một chất điểm dao động điều hoà dọc trục Ox quanh VTCB O với biên độ A và chu kì T. Theo phương trình với x tính bằng cm và t tính bằng s. Hãy xác định quãng đường nhỏ nhất vật đi được trong t =0,625 (s)
Một chất điểm dao động điều hoà dọc trục Ox quanh VTCB O với biên độ A và chu kì T. Theo phương trình với x tính bằng cm và t tính bằng s. Hãy xác định quãng đường nhỏ nhất vật đi được trong t = 0,8125(s)
Vật dao động điều hòa theo phương trình : . Tốc độ của vật sau khi đi quãng đường S = 2 cm (kể từ t = 0) là?
Một người quan sát một chiếc phao trên mặt biển, thấy nó nhô cao 10 lần trong khoảng thời gian . Chu kì của sóng biển là?
Một đồng hồ quả lắc chạy đúng giờ trên mặt đất ở nhiệt độ . Biết hệ số nở dài dây treo con lắc là . Khi nhiệt độ ở đó thì sau một ngày đêm, đồng hồ sẽ chạy như thế nào ?
Con lắc của một đồng hồ quả lắc có chu kì 2s ở nhiệt độ . Nếu tăng nhiệt độ lên đến thì đồng hồ đó trong một ngày đêm chạy nhanh hay chậm bao nhiêu ? Cho hệ số nở dài là
Một đồng hồ quả lắc chạy nhanh 8,64s trong một ngày tại một nơi trên mặt biển và ở nhiệt độ . Thanh treo con lắc có hệ số nở dài . Cùng vị trí đó, đồng hồ chạy đúng ở nhiệt độ là
Một đồng hồ chạy đúng ở nhiệt độ = . Nếu nhiệt độ tăng đến thì mỗi ngày đêm đồng hồ nhanh hay chậm bao nhiêu ? Cho hệ số nở dài của dây treo con lắc là
Một đồng hồ con lắc đếm giây có chu kì T = 2s mỗi ngày chạy nhanh 120 giây. Hỏi chiều dài con lắc phải điều chỉnh như thế nào để đồng hồ chạy đúng.
Một con lắc đơn được treo vào trần một thang máy tại nơi có Khi thang đứng yên thì chu kì dao động nhỏ của con lắc là 2s. Thang máy đi lên nhanh dần đều với gia tốc thì tần số dao động của con lắc bằng
Một con lắc đơn được treo vào trần một thang máy tại nơi có . Khi thang đứng yên thì chu kì dao động nhỏ của con lắc là 2s. Thang máy đi xuống đều thì tần số dao động của con lắc bằng
Một con lắc đơn được treo vào trần một thang máy tại nơi có . Khi thang đứng yên thì chu kì dao động nhỏ của con lắc là 2s. Thang máy đi lên chậm dần đều với gia tốc thì con lắc dao động với tần số bằng
Một con lắc đơn dao động điều hoà với phương trình = 0,14cos()(rad). Thời gian ngắn nhất để con lắc đi từ vị trí có li độ góc 0,07(rad) đến vị trí biên gần nhất là
Một con lắc đơn dao động điều hoà với phương trình s = 6cos(0,5 t- )(cm). Khoảng thời gian ngắn nhất để con lắc đi từ vị trí có li độ s = 3cm đến li độ cực đại = 6cm là
Một con lắc đơn dao động nhỏ với biên độ 4cm. Khoảng thời gian giữa hai lần liên tiếp vận tốc của vật đạt giá trị cực đại là 0,05s. Khoảng thời gian ngắn nhất để nó đi từ vị trí có li độ = 2cm đến li độ = 4cm là
Cho con lắc của đồng hồ quả lắc có = . Khi ở mặt đất có nhiệt độ , đưa con lắc lên độ cao h = 640m so với mặt đất, ở đó nhiệt độ là 5C. Trong một ngày đêm đồng hồ chạy nhanh hay chậm bao nhiêu ?
Cho một con lắc đơn có chiều dài dao động điều hoà với chu kì =1,2s; con lắc đơn có chiều dài dao động với chu kì =1,6s. Hỏi con lắc đơn có chiều dài dao động tại nơi đó với tần số bằng bao nhiêu ?
Tại một nơi trên mặt đất, con lắc đơn có chiều dài dao động với tần số 3Hz, con lắc đơn có chiều dài dao động với tần số 4Hz. Con lắc có chiều dài sẽ dao động với tần số là
Một con lắc đơn có độ dài bằng . Trong khoảng thời gian nó thực hiện được 6 dao động. Người ta giảm bớt độ dài của nó 16cm. Cùng trong khoảng thời gian như trước, nó thực hiện được 10 dao động. Cho g = 9,80m/s2. Độ dài ban đầu và tần số ban đầu của con lắc lần lượt là
Quả cầu khối lượng gắn vào đầu một lò xo có độ cứng treo thẳng đứng, quả cầu được nối vào đầu A của một dây AB căng ngang. Giả sử lực căng dây không làm ảnh hưởng đến chuyển động của quả cầu. Kích thích cho quả cầu dao động tự do theo phương thẳng đứng, ta thấy trên dây có sóng dừng với 6 bó sóng. Biết dây AB dài . Tốc độ truyền sóng trên dây là:
Một ôtô chuyển động nửa đoạn đường đầu tiên với vận tốc nửa đoạn đường còn lại chuyển động với vận tốc
Một ôtô chuyển động trong 1/3 quãng đường đầu tiên với vận tốc , 1/3 quãng đường kế tiếp với vận tốc , phần còn lại ôtô chuyển động với vận tốc .
Một ôtô chuyển động trong đầu với vận tốc , còn lại ôtô chuyển động với vận tốc .
Một ôtô chuyển động trong 5 giờ, biết trong hai giờ đầu ôtô chuyển động với vận tốc , 3 giờ còn lại ôtô chuyển động với vận tốc .
Trong mạch dao động LC có điện trở thuần không đáng kể. Sau những khoảng thời gian bằng thì năng lượng điện trường lại bằng năng lượng từ trường. Chu kỳ dao động của mạch là
Một mạch dao động lý tưởng LC, năng lượng từ trường và năng lượng điện trường cứ sau 1ms lại bằng nhau. Chu kì dao động của mạch dao động bằng
Trong mạch dao động LC lý tưởng, biểu thức điện tích trên hai bản tụ là . Kể từ thời điểm t = 0 s cho đến khi năng lượng từ trường cực đại lần đầu tiên thì tụ điện đã phóng được một điện lượng bằng
Mạch dao động LC, cuộn dây thuần cảm, cứ sau khoảng thời gian thì năng lượng điện trường và năng lượng từ trường lại bằng nhau. Tần số của mạch là
Một tụ điện có điện dung được tích điện đến hiệu điện thế . Sau đó hai đầu tụ được đấu vào hai đầu của một cuộn dây có độ tự cảm bằng 0,5H. Bỏ qua điện trở thuần của cuộn dây và dây nối. Lần thứ hai điện tích trên tụ bằng một nửa điện tích lúc đầu là ở thời điểm nào? (tính từ lúc khi t = 0 là lúc đấu tụ điện với cuộn dây).
Một tụ điện có điện dung được tích điện đến một hiệu điện thế xác định. Sau đó nối hai bản tụ điện vào hai đầu một cuộn dây thuần cảm có độ tự cảm 1 H. Bỏ qua điện trở của các dây nối, lấy . Sau khoảng thời gian ngắn nhất là bao nhiêu (kể từ lúc nối) điện tích trên tụ điện có giá trị bằng một nửa giá trị ban đầu?
Một mạch dao động điện từ LC lí tưởng gồm cuộn cảm thuần có độ tự cảm và tụ điện có điện dung . Trong mạch có dao động điện từ tự do. Khoảng thời gian giữa hai lần liên tiếp mà điện tích trên một bản tụ điện có độ lớn cực đại là
Một mạch dao động điện từ lí tưởng đang có dao động điện từ tự do. Tại thời điểm t = 0, điện tích trên một bản tụ điện cực đại. Sau khoảng thời gian ngắn nhất thì điện tích trên bản tụ này bằng một nửa giá trị cực đại. Chu kì dao động riêng của mạch dao động này là
Trong mạch dao động LC lí tưởng đang có dao động điện từ tự do. Thời gian ngắn nhất để năng lượng điện trường giảm từ giá trị cực đại xuống còn một nửa giá trị cực đại là . Thời gian ngắn nhất để điện tích trên tụ giảm từ giá trị cực đại xuống còn một nửa giá trị đó là
Một mạch dao động điện từ lí tưởng đang có dao động điện từ tự do. Biết điện tích cực đại trên một bản tụ điện là và cường độ dòng điện cực đại trong mạch là . Thời gian ngắn nhất để điện tích trên một bản tụ giảm từ giá trị cực đại đến nửa giá trị cực đại là
Một mạch dao động lí tưởng đang có dao động điện từ tự do với chu kì dao động T. Tại thời điểm t = 0, điện tích trên một bản tụ điện đạt giá trị cực đại. Điện tích trên bản tụ này bằng 0 ở thời điểm đầu tiên (kể từ t = 0) là
Một máy định vị vô tuyến nằm cách mục tiêu 60 km. Máy nhận được tín hiệu trở về từ mục tiêu kể từ lúc phát sau khoảng thời gian là
Đoàn tàu Thống nhất Bắc Nam xuất phát từ ga Hà Nội vào lúc 19h00, ngày 18 tháng 7 năm 2019, tới ga Sài Gòn vào lúc 4h00 ngày 20 tháng 7 năm 2019. Trong thời gian đó tàu phải nghỉ ở một số ga để trả khách mất 39 phút. Không kể thời gian tàu nghỉ ở các ga, khoảng thời gian tàu Thống nhất Bắc Nam chạy từ ga Hà Nội tới ga Sài Gòn là bao nhiêu?

Một người xem đồng hồ thì thấy đồng hồ chỉ 10:00 am. Hỏi mốc thời gian trên được tính từ lúc nào?
Một con lắc đơn có chiều dài và khối lượng m = 100g. Kéo con lắc lệch khỏi vị trí cân bằng một góc rồi thả nhẹ cho dao động. Sau 20 chu kì thì biên độ góc chỉ còn là . Lấy . Để con lắc dao động duy trì với biên độ góc thì phải dùng bộ máy đồng hồ để bổ sung năng lượng có công suất trung bình là
Cho một con lắc lò xo có độ cứng là k, khối lượng vật m = 1kg. Treo con lắc trên trần toa tầu ở ngay phía trên trục bánh xe. Chiều dài thanh ray là L=12,5m. Tàu chạy với vận tốc 54km/h thì con lắc dao động mạnh nhất. Độ cứng của lò xo là
Hai lò xo có độ cứng mắc nối tiếp, đầu trên mắc vào trần một toa xe lửa, đầu dưới mang vật m = 1kg. Khi xe lửa chuyển động với vận tốc 90km/h thì vật nặng dao động mạnh nhất. Biết chiều dài mỗi thanh ray là 12,5m, . Coi chuyển động của xe lửa là thẳng đều. Độ cứng bằng
Một chiếc xe đẩy có khối lượng m được đặt trên hai bánh xe, mỗi gánh gắn một lò xo có cùng độ cứng k = 200N/m. Xe chạy trên đường lát bê tông, cứ 6m gặp một rãnh nhỏ. Với vận tốc v = 14,4km/h thì xe bị rung mạnh nhất. Lấy . Khối lượng của xe bằng
Hai lò xo có độ cứng lần lượt mắc nối tiếp với nhau. Vật nặng m = 1kg, đầu trên của là lo mắc vào trục khuỷu tay quay như hình vẽ. Quay đều tay quay, ta thấy khi trục khuỷu quay với tốc độ 300vòng/min thì biên độ dao động đạt cực đại. Biết . Độ cứng bằng
Một vật chuyển động thẳng đều với phương trình:
Lúc 7h sáng một xe chuyển động với phương trình: . Hãy xác định các yêu cầu sau:
Lúc 7h sáng có hai xe ô tô chuyển động với phương trình như sau: . Hãy xác định các yêu cầu sau:
Một xe xuất phát từ thành phố A lúc 7 giờ sáng, chuyển động thẳng đều đến thành phố B với vận tốc ,
Một ô tô xuất phát từ A lúc 6h am chuyển động thẳng đều tới B lúc 8h am khoảng cách từ A đến B là
Một vận động viên xe đạp xuất phát tại A lúc 6 giờ sáng, chuyển động thẳng đều tới B với vận tốc . Khoảng cách từ A đến B là .
Một người chạy bộ từ A đến B lúc 5 giờ sáng với vận tốc cùng lúc có một người chạy từ B đến A với vận tốc . Biết khoảng cách từ A đến B là .
Một xe xuất phát từ thành phố A lúc 7 giờ sáng, chuyển động thẳng đều đến thành phố B với vận tốc .Chọn trục tọa độ trùng với đường đi, chiều dương là chiều chuyển động của xe, gốc tọa độ tại A, gốc thời gian là lúc xe bắt đầu xuất phát (lúc 7 giờ).
Hai thành phố A và B cách nhau . Lúc sáng một xe ô tô xuất phát từ C đi thành phố B. Biết rằng C cách thành phố A và C nằm giữa thành phố A và B. Tốc độ chuyển động của xe là
Chọn gốc thời gian là lúc xe xuất phát, gốc tọa độ tại A, chiều dương từ A đến B.
Trên một đường thẳng có hai xe chuyển động ngược chiều nhau, khởi hành cùng một lúc từ A và B cách nhau ; xe đi từ A có tốc độ và xe đi từ B có tốc độ . Lấy gốc tọa độ tại A, chiều dương từ A đến B, gốc thời gian lúc hai xe bắt đầu khởi hành.
Lúc 7 giờ sáng hai xe cùng khởi hành một lúc từ hai địa điểm A và B trên một đường thẳng cách nhau chuyển động đều, cùng hướng từ A đến B. Tốc độ của xe đi từ A là , xe đi từ B là . Lấy gốc thời gian là lúc hai xe bắt đầu xuất phát, gốc tọa độ tại A, chiều dương từ A đến B.
Một chất điểm chuyển động thẳng đều có phương trình chuyển động là
Trong chuyển động thẳng đều của một vật thì
Chọn câu trả lời sai. "Chuyển động thẳng đều là chuyển động có ..."
Điều nào sau đây là không đúng khi nói về tọa độ của vật chuyển động thẳng đều?
Có hai vật chuyển động thẳng đều trên cùng trục Ox, xuất phát cùng vị trí và cùng thời điểm, ngược chiều với nhau, các vận tốc có cùng độ lớn bằng . Trong hệ trục tOx, chúng được biểu diễn bởi hai đoạn thẳng như thế nào?
Chọn kết luận sai: Trong chuyển động thẳng đều, ...
Đồ thị toạ độ - thời gian của chuyển động thẳng đều là đường thẳng như thế nào?
Trong chuyển động thẳng đều vector vận tốc tức thời và vector vận tốc trung bình trong khoảng thời gian bất kỳ ...
Một người đi bộ trên một đường thẳng với vận tốc không đổi . Thời gian để người đó đi hết quãng đường là
Một vật chuyển động thẳng đều với phương trình ( được tính bằng , được tính bằng ). Ban đầu vật cách mốc tọa độ bao xa?
Chuyển động thẳng đều là chuyển động thẳng trong đó ...
Một vật chuyển động thẳng đều với phương trình . Tại tọa độ của vật là bao nhiêu?
Một xe ô tô lúc 7h00 sáng xuất phát từ A đến B với vận tốc không đổi là . Lấy gốc tọa độ tại A, chiều dương là chiều từ A đến B, gốc thời gian là lúc 7h00 sáng. Phương trình chuyển động của vật là
Một chất điểm chuyển động thẳng đều theo chiều dương của trục toạ độ với vận tốc có độ lớn bằng tại thời điểm ban đầu chất điểm ở vị trí cách gốc toạ độ về phía âm của trục toạ độ. Phương trình chuyển động của chất điểm là
Một người đi xe máy khởi hành từ thị trấn A lúc 6 giờ sáng để đến thị trấn B cách đó người này đến B lúc 9 giờ sáng. Giả sử chuyển động là thẳng đều. Chọn gốc thời gian lúc 6 giờ sáng, gốc toạ độ tại B, chiều dương từ A đến B, phương trình chuyển động trong trường hợp này là
Một bọt khí chuyển động thẳng đều trong ống AB dài và đi từ A đến B mất 1 phút. Chọn gốc thời gian lúc bọt khí qua A, gốc toạ độ tại A và chiều dương từ B đến A, phương trình chuyển động
Lúc 7h00 sáng một người đi xe đạp đuổi theo một người đi bộ đã đi được . Cả hai chuyển động thẳng đều với vận tốc và . Người đi xe đạp đuổi kịp người đi bộ vào thời điểm và vị trí nào sau đây?
Lúc 9h một xe khởi hành từ A đi về B theo chuyển động thẳng đều với vận tốc . Nửa giờ sau, một xe đi từ B về A với vận tốc . Cho . Xác định thời điểm hai xe gặp nhau.
Phương trình chuyển động của một chất điểm dọc theo trục Ox có dạng: ; x tính bằng km; t tính bằng giờ. Tọa độ của chất điểm sau 4 giờ là bao nhiêu?
Hai người đi bộ theo một chiều trên một đường thẳng AB, xuất phát cùng lúc tại vị trí A, với vận tốc lần lượt là và người thứ hai đến B sớm hơn người thứ nhất 5,5 phút. Quãng đường AB dài bao nhiêu?
Một người đi xe máy khởi hành từ thị trấn A lúc 6 giờ sáng để đến thị trấn B cách đó người này đến B lúc 9 giờ sáng. Giả sử chuyển động là thẳng đều. Chọn gốc thời gian lúc 6 giờ sáng, gốc toạ độ tại A, chiều dương từ A đến B, phương trình chuyển động
Một bọt khí chuyển động thẳng đều trong ống AB dài và đi từ A đến B mất 1phút. Chọn gốc thời gian lúc bọt khí qua B, gốc toạ độ tại B và chiều dương từ A đến B, phương trình chuyển động
Trong các chuyển động thẳng đều có phương trình chuyển động sau đây, phương trình nào cho biết gốc thời gian được chọn lúc vật qua vị trí cách gốc toạ độ 2 cm
Một vật chuyển động với phương trình .
Một chất điểm chuyển động dọc theo hai cạnh liên tiếp của một tam giác đều cạnh mất . Chọn kết luận sai:
Một ôtô chuyển động trong 6 giờ. Trong 2 giờ đầu ôtô chuyển động với vận tốc trong 3 giờ kế tiếp ô tô chuyển động với vận tốc trong giờ còn lại ôtô chuyển động với vận tốc .
Một ô tô chuyển động với vận tốc trên nửa đoạn đường đầu, trong nửa đoạn đường còn lại ôtô chuyển động nửa thời gian đầu với vận tốc và nửa thời gian còn lại ôtô chuyển động với vận tốc .
Một chiếc xe trong 2 giờ đầu chuyển động với tốc độ trong 3 giờ tiếp theo chuyển động với tốc độ .
Một vận động viên chạy hết một vòng quanh sân vận động có chu vi mất . Chọn kết luận đúng:
Một ô tô chạy từ tỉnh A đến tỉnh B. Trong nửa đoạn đường đầu, xe chuyển động với vận tốc . Trong nửa đoạn đường sau xe chạy với vận tốc . Hỏi tốc độ trung bình của xe trên đoạn đường AB là bao nhiêu?
Một ôtô chạy trên đường thẳng. Ở đoạn đầu của đường đi, ôtô chạy với vận tốc không đổi , ở đoạn sau của đường đi, ôtô chạy với vận tốc . Hỏi vận tốc trung bình trên cả đoạn đường là bao nhiêu?
Một máy bay cất cánh từ Hà Nội đi Bắc Kinh vào hồi 9 giờ 30 phút theo giờ Hà Nội và đến Bắc Kinh vào lúc 14 giờ 30 phút cùng ngày theo giờ địa phương. Biết rằng giờ Bắc Kinh nhanh hơn giờ Hà Nội 1 giờ. Biết vận tốc trung bình của máy bay là . Coi máy bay chuyển động theo đường thẳng. Hỏi khoảng cách từ Hà Nội đến Bắc Kinh là bao nhiêu?
Cho hệ tọa độ và các điểm như hình vẽ. Quãng đường của vật khi vật đi từ B đến A là

Cho hệ tọa độ và các điểm như hình vẽ. Quãng đường của vật khi vật đi từ A đến B rồi trở lại O.

Cho hệ tọa độ và các điểm như hình vẽ. Một vật đi từ A đến B rồi quay trở lại O mất tổng thời gian là . Xác định tốc độ trung bình và vận tốc trung bình của vật?

Cho hệ tọa độ và các điểm như hình vẽ. Một vật đi từ O đến A sau đó quay về B mất tổng thời gian là . Xác định vận tốc trung bình và tốc độ trung bình của vật trong khoảng thời gian trên?

Phát biểu nào sau đây là đúng nhất khi nói về chuyển động cơ học?
Trong các chuyển động sau đây, chuyển động nào thì vật được xem là chất điểm?
Xét một chất điểm chuyển động thẳng từ điểm có toạ độ đến điểm có tọa độ . Độ dời của chất điểm là:
Vật chuyển động thẳng đều có đồ thị toạ độ - thời gian như hình vẽ. Kết luận nào rút ra từ đồ thị là sai.

Một vật chuyển động với phương trình .
Một vật chuyển động thẳng đều có đồ thị tọa
Có hai xe chuyển động thẳng đều có đồ thị tọa độ như hình vẽ:
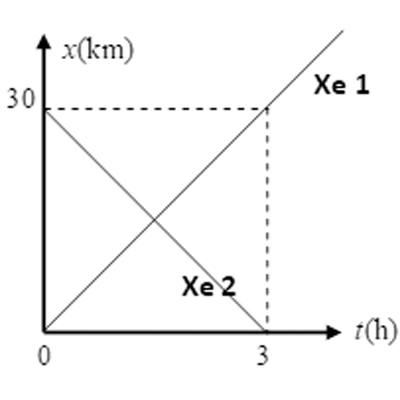
Vật chuyển động thẳng đều có đồ thị toạ độ - thời gian như hình vẽ. Kết luận nào rút ra từ đồ thị là sai.
Trong tác dụng của dòng điện xoay chiều, tác dụng không phụ thuộc vào chiều của dòng điện là tác dụng?
Trường hợp nào dưới đây có thể dùng đồng thời cả hai lọai dòng điện xoay chiều và dòng điện không đổi?
Cho mạch R, L, C mắc nối tiếp. Với các giá trị đã cho thì sớm pha hơn điện áp giữa hai đầu đoạn mạch một góc . Nếu ta tăng điện trở R thì:
Một vật thực hiện đồng thời hai dao động điều hoà cùng phương, cùng tần số với phương trình: . Gia tốc của vật tại thời điểm là
Một vật rơi tự do từ độ cao 80m xuống đất, . Tính tổng thời gian từ lúc vật rơi đến khi chạm đất.
Một vật rơi tự do từ độ cao 80m xuống đất, . Tính vận tốc của vật lúc vừa chạm đất.
Một vật rơi tự do từ độ cao S xuống mặt đất. Cho biết trong 2 giây cuối cùng trước khi chạm đất, vật rơi được quãng đường bằng một phần tư độ cao S. Lấy .
Một vật được thả rơi không vận tốc đầu khi vừa chạm đất có v = 60m/s, . Xác định quãng đường rơi của vật, tính thời gian rơi của vật.
Một người đứng trên tòa nhà có độ cao 120 m, ném một vật thẳng đứng xuống dưới với vận tốc 10 m/s cho . Kể từ lúc ném, sau bao lâu vật chạm đất?
Một người đứng trên tòa nhà có độ cao 120 m, ném một vật thẳng đứng xuống dưới với vận tốc 10 m/s cho . Tính vận tốc của vật lúc vừa chạm đất.
Một vật rơi tự do khi chạm đất thì vật đạt vận tốc 40 m/s. Hỏi vật được thả rơi từ độ cao nào? biết .
Người ta thả một vật rơi tự do từ một tòa tháp thì sau 20s vật chạm đất cho . Tính độ cao của tòa tháp.
Người ta thả một vật rơi tự do từ một tòa tháp thì sau 20s vật chạm đất cho . Vận tốc khi chạm đất là bao nhiêu?
Người ta thả một vật rơi tự do từ một tòa tháp thì sau 20 s vật chạm đất cho . Độ cao của vật sau khi vật thả được 4s là
Một vật được thả rơi từ độ cao 1280 m so với mặt đất. Lấy . Tìm thời gian để vật rơi từ lúc thả đến lúc chạm đất.
Một vật được thả rơi từ độ cao 1280 m so với mặt đất. Lấy . Tìm vận tốc của vật khi chạm đất.
Một vật được thả rơi từ độ cao 1280 m so với mặt đất. Lấy . Sau khi rơi được 2s thì vật còn cách mặt đất bao nhiêu?
Một vật được thả rơi từ độ cao 1280 m so với mặt đất. Lấy . Khi vận tốc của vật là 40 m/s thì vật còn cách mặt đất bao nhiêu? Còn bao lâu nữa thì vật chạm đất?
Một người thả một hòn đá từ tầng 2 độ cao h xuống đáy, hòn đá rơi trong 2s. Nếu thả hòn đá đó từ tầng 32 có độ cao h’=16h thì thời gian rơi là bao nhiêu?
Một vật rơi không vận tốc đầu từ đỉnh tòa nhà chung cư có độ cao 320m xuống đất. Cho . Tìm vận tốc lúc vừa chạm đất và thời gian của vật rơi.
Một vật rơi không vận tốc đầu từ đỉnh tòa nhà chung cư có độ cao 320m xuống đất. Cho . Tính quãng đường vật rơi được trong 2s đầu tiên và 2s cuối cùng.
Một vật rơi tự do tại một địa điểm có độ cao 500m, biết . Tính thời gian vật rơi hết quãng đường.
Một vật rơi tự do tại một địa điểm có độ cao 500m biết . Tính quãng đường vật rơi được trong 5s đầu tiên.
Một vật rơi tự do tại một địa điểm có độ cao 500m biết . Tính quãng đường vật rơi trong giây thứ 5.
Cho một vật rơi tự do từ độ cao h. Trong 2s cuối cùng trước khi chạm đất, vật rơi được quãng đường 60m. Tính thời gian rơi và độ cao h của vật. Biết .
Cho một vật rơi tự do từ độ cao h. Biết rằng trong 2s cuối cùng vật rơi được quãng đường bằng quãng đường đi trong 5s đầu tiên, . Tìm độ cao lúc thả vật và thời gian vật rơi.
Cho một vật rơi tự do từ độ cao h. Biết rằng trong 2s cuối cùng vật rơi được quãng đường bằng quãng đường đi trong 5s đầu tiên, . Tìm vận tốc của vật lúc vừa chạm đất.
Cho một vật rơi tự do từ độ cao 800m biết . Tính thời gian vật rơi 80m đầu tiên.
Cho một vật rơi tự do từ độ cao 800m biết . Tính thời gian vật rơi được 100m cuối cùng.
Một vật rơi tự do từ độ cao h xuống mặt đất. Biết rằng trong 2s cuối cùng vật rơi được đoạn bằng độ cao h. Lấy . Hỏi thời gian rơi của vật từ độ cao h xuống mặt đất là bao nhiêu?
Một vật được thả rơi tự do không vận tốc đầu từ độ cao h biết trong 7s cuối cùng vật rơi được 385m cho . Xác định thời gian và quãng đường rơi.
Một vật được thả rơi tự do không vận tốc đầu từ độ cao h biết trong 7s cuối cùng vật rơi được 385m cho . Tính đoạn đường vật đi được trong giây thứ 6.
Một vật được thả rơi tự do không vận tốc đầu từ độ cao h biết trong 7s cuối cùng vật rơi được 385m cho . Tính thời gian cần thiết để vật rơi 85m cuối cùng.
Một vật rơi tự do từ độ cao h trong 10s thì tiếp đất. Quãng đường vật rơi trong 2s cuối cùng là bao nhiêu? cho
Một vật rơi tự do không vận tốc đầu từ độ cao 80m xuống đất biết . Tính thời gian rơi và tốc độ của vật khi vừa chạm đất.
Một vật được thả rơi tự do không vận tốc đầu từ độ cao h so với mặt đất. Cho . Tốc độ của vật khi chạm đất là 60m/s. Tính độ cao h, thời gian từ lúc vật bắt đầu rơi đến khi vật chạm đất.
Một vật được thả rơi tự do không vận tốc đầu từ độ cao h so với mặt đất. Cho . Tốc độ của vật khi chạm đất là 60m/s. Tính quãng đường vật rơi trong bốn giây đầu và trong giây thứ tư.
Một vật được thả rơi tự do không vận tốc đầu từ độ cao h so với mặt đất. Cho . Thời gian vật rơi hết độ cao h là 8 giây. Tính độ cao h, tốc độ của vật khi vật chạm đất.
Một vật được thả rơi tự do không vận tốc đầu từ độ cao h so với mặt đất. Cho . Thời gian vật rơi hết độ cao h là 8 giây. Tính quãng đường vật rơi trong giây cuối cùng trước khi chạm đất.
Một vật được thả rơi tự do không vận tốc đầu từ độ cao h so với mặt đất. Thời gian vật rơi 10 m cuối cùng trước khi chạm đất là 0,2s. Tính độ cao h, tốc độ của vật khi chạm đất. Cho
Một vật rơi tự do không vận tốc đầu tại nơi có gia tốc trọng trường g. Trong giây thứ 3, quãng đường rơi được là 25m và tốc độ của vật khi vừa chạm đất là 40m/s. Tính g và độ cao nơi thả vật.
Một vật được thả rơi tự do không vận tốc đầu từ độ cao h so với mặt đất tại nơi có gia tốc trọng trường . Quãng đường vật rơi trong nửa thời gian sau dài hơn quãng đường vật rơi trong nửa thời gian đầu 40m. Tính độ cao h và tốc độ của vật khi chạm đất.
Tại M cách mặt đất ở độ cao h, một vật được ném thẳng đứng lên đến vị trí N cao nhất rồi rơi xuống qua P có cùng độ cao với M. Bỏ qua mọi lực cản thì
Một viên bi được ném thẳng đứng lên trên với vận tốc ban đầu . Khi viên bi chuyển động, đại lượng có độ lớn không đổi là:
Trong trường hợp nào dưới đây, quãng đường vật đi được tỉ lệ thuận với thời gian chuyển động?
Chuyển động nào dưới đây được xem là rơi tự do?
Đặc điểm nào dưới đây không phải là đặc điểm của chuyển động rơi tự do của các vật?
Chuyển động của vật rơi tự do không có tính chất nào sau đây?
Thí nghiệm của nhà bác học Galileo ở tháp nghiêng thành Pisa và thí nghiệm với ống của nhà bác học Newton chứng tỏ. Kết quả nào sau đây là đúng:
Trường hợp nào sau đây có thể coi là sự rơi tự do?
Một quả cầu ném thẳng đứng lên trên. Tại điểm cao nhất của quỹ đạo phát biểu nào sau đây là đúng?
Hai bạn Giang và Vân đi chơi ở một tòa nhà cao tầng. Từ tầng 19 của tòa nhà, Giang thả rơi viên bi A thì 1s sau thì Vân thả rơi viên bi B ở tầng thấp hơn 10m. Hai viên bi sẽ gặp nhau lúc nào, ở đâu? Cho
Từ một đỉnh tháp cao 20m, người ta buông một vật. Sau 2s thì người ta lại buông vật thứ 2 ở tầng thấp hơn đỉnh tháp 5m. cho . Hai vật có chạm đất cùng một lúc hay không và vận tốc lúc chạm đất của mỗi vật là bao nhiêu?
Ở một tầng tháp cách mặt đất 45m, một người thả rơi một vật. Một giây sau, người đó ném vật thứ hai xuống theo hướng thẳng đứng. Hai vật chạm đất cùng lúc. Tính vận tốc ném vật thứ hai.
Một viên bi A được thả rơi từ độ cao 30m. Cùng lúc đó, một viên bi B được bắn theo phương thẳng đứng từ dưới đất lên với vận tốc 25m/s tới va chạm vào bi A. Cho . Bỏ qua sức cản không khí. Tính thời điểm khi 2 viên bi gặp nhau.
Một viên bi A được thả rơi từ độ cao 30m. Cùng lúc đó, một viên bi B được bắn theo phương thẳng đứng từ dưới đất lên với vận tốc 25m/s tới va chạm vào bi A. Cho . Bỏ qua sức cản không khí. Vận tốc viên bi B khi hai viên bi gặp nhau.
Người ta thả rơi tự do hai vật A và B ở cùng một độ cao. Vật B được thả rơi sau vật A một thời gian là 0,1s. Hỏi sau bao lâu kể từ lúc thả vật A thì khoảng cách giữa chúng là 1m. Lấy .
Một ống Rơnghen trong 20 người ta thấy có electron đập vào đôi catôt. Cho biết điện tích của electron là . Cường độ dòng điện qua ống là
Công suất của một nguồn sáng là . Biết nguồn phát ra ánh sáng đơn sắc đơn sắc có bước sóng . Cho hằng số Plăng và tốc độ ánh sáng trong chân không . Số phôtôn phát ra từ nguồn sáng trong một phút là
Một nguồn sáng có công suất phát ra ánh sáng tỏa ra đều theo mọi hướng mà mỗi phô tôn có năng lượng . Một người quan sát đứng cách nguồn sáng 300 km. Bỏ qua sự hấp thụ ánh sáng bởi khí quyển. Tính số phôtôn lọt vào mắt người quan sát trong mỗi giây. Coi bán kính con ngươi là 2 mm.
Một nguồn sáng có công suất 2,4 W, phát ra ánh sáng có bước sóng 0,6 µm tỏa ra đều theo mọi hướng. Hãy xác định khoảng cách xa nhất người còn trông thấy được nguồn sáng này. Biết rằng mắt còn cảm nhận được ánh sáng khi có ít nhất 100 phôtôn lọt vào mắt trong mỗi giây. Cho hằng số Plăng và tốc độ ánh sáng trong chân không . Coi đường kính con ngươi vào khoảng 4 mm. Bỏ qua sự hấp thụ ánh sáng bởi khí quyển.
Ánh sáng đơn sắc với bước sóng m chiếu vuông góc vào một diện tích 4 cm2. Cho hằng số Plăng và tốc độ ánh sáng trong chân không . Nếu cường độ ánh sáng bằng thì số photon đập lên diện tích ấy trong một đơn vị thời gian là
Cho chùm hẹp các electron quang điện có tốc độ bay dọc theo đường sức trong một điện trường đều có cường độ 9,1 (V/m) sao cho hướng của vận tốc ngược hướng với điện trường. Tính quãng đường đi được sau thời gian 1000 ns. Biết khối lượng và điện tích của êlectron lần lượt là kg và .
Hai bản kim loại phẳng có độ dài 30 cm đặt nằm ngang, song song cách nhau một khoảng 16 cm. Giữa hai bản tụ có một hiệu điện thế 12 (V). Hướng một chùm hẹp các electron quang điện có tốc độ theo phương ngang vào giữa hai bản tại điểm O cách đều hai bản. Khối lượng của electron là . Tính thời gian electron chuyển động trong tụ.
Một nguồn bức xạ có công suất phát sáng 1 W phát ánh sáng đơn sắc có bước sóng 0,7 µm. Cho hằng số Plăng và tốc độ ánh sáng trong chân không lần lượt là , . số phôtôn của nó phát ra trong 1 giây là:
Một ngọn đèn phát ánh sáng đơn sắc có công suất trong 10 s phát ra được phôtôn. Cho hằng số Plăng và tốc độ ánh sáng trong chân không . Bức xạ này có bước sóng là
Chiếu một chùm bức xạ điện từ có bước sóng 0,4 μm vào một bản M (công thoát electron là 1,4 eV) của một tụ điện phẳng. Đối với các electron bứt ra có động năng ban đầu cực đại thì động năng đó bằng năng lượng phôtôn hấp thụ được trừ cho công thoát. Hiệu điện thế hãm nhỏ nhất hai bản tụ phải bằng bao nhiêu để electron thoát ra trên bản M bay trong khoảng chân không giữa hai bản tụ và dừng ngay trên bản N.
Cho chùm hẹp các electron quang điện có tốc độ bay dọc theo đường sức trong một điện trường đều có cường độ 9,1 (V/m) sao cho hướng của vận tốc cùng hướng với điện trường. Tính quãng đường đi được sau thời gian 1000 ns. Biết khối lượng và điện tích của electron lần lượt là và .
Tách một chùm hẹp các electron quang điện có tốc độ và cho đi vào điện trường đều của một tụ điện phẳng tại điểm O cách đều hai bản tụ và phương song song với hai bản tụ. Biết hiệu điện thế giữa hai bản tụ 0,455 (V), khoảng cách giữa hai bản tụ 2 cm, chiều dài của tụ 5 cm và khối lượng của electron là . Tính thời gian electron chuyển động trong tụ.
Một bánh xe quay đều 100 vòng trong 4 giây. Chu kì quay của bánh xe là?
Điều nào sau đây là sai khi nói về vật chuyển động tròn đều?
Trong các chuyển động tròn đều
Trong máy cyclotron các proton khi được tăng tốc đến tốc độ V thì chuyển động tròn đều với bán kính R. Chu kì quay của proton là
Một vật điểm chuyển động trên đường tròn bán kính 10 (cm) với tần số không đổi 10 (vòng/s). Tính chu kì, tần số góc, tốc độ dài.
Một xe tải đang chuyển động thẳng đều có có bánh xe có bán kính . Tính chu kì, tần số, tốc độ góc của đầu van xe.
Một xe máy đang chạy, có một điểm nằm trên vành ngoài của lốp xe máy cách trục bánh xe . Bánh xe quay đều với tốc độ . Số vòng bánh xe quay để số chỉ trên đồng hồ tốc độ của xe sẽ nhảy 1 số ứng với 1 (km) và thời gian quay hết số vòng ấy là bao nhiêu? Biết
Cho một chiếc đu quay có bán kính quay quanh một trục cố định. Thời gian quay hết 4 vòng là . Hãy tính tốc độ góc, tốc độ dài, gia tốc hướng tâm của điểm ngoài cùng đu quay.
Một đĩa quay đều quanh trục qua tâm O, với vận tốc qua tâm là . Tính tốc độ góc, chu kì, tốc độ dài, gia tốc hướng tâm của 1 điểm trên đĩa cách tâm , .
Việt Nam phóng một vệ tinh nhân tạo lên quỹ đạo có độ cao là , thì vệ tinh có vận tốc là . Biết bán kính trái đất . Xác định thời gian để vệ tinh quay hết một vòng và gia tốc hướng tâm của vệ tinh
Nước Việt Nam phóng vệ tinh lên quỹ đạo. Sau khi ổn định, vệ tinh chuyển động tròn đều với ở độ cao so với mặt đất. Bán kính TĐ là . Tính tốc độ góc, chu kì, tần số của vệ tinh.
Một bánh xe quay đều trong . Chu kỳ quay của bánh xe là
Một đĩa tròn bán kính quay đều quanh trục đi qua tâm và vuông góc với đĩa. Đĩa quay 50 vòng trong . Tốc độ dài của một điểm nằm trên mép đĩa bằng
Một quạt máy khi hoạt động ở một tốc độ xác định quay được trong thời gian . Tốc độ góc của cánh quạt là
Một đoàn tàu bắt đầu chuyển động nhanh dần đều vào một cung đường tròn với vận tốc . Bán kính đường tròn và cung đường dài . Đoàn tàu chạy hết cung đường này mất . Gia tốc toàn phần của đoàn tàu ở cuối cung đường bằng
Lúc 7h hai xe ô tô khởi hành từ hai điểm AB cách nhau 24km, chuyển động thẳng nhanh dần đều và ngược chiều hướng về nhau. Ô tô đi từ A có gia tốc , ô tô đi từ B có gia tốc . Xác định thời gian và địa điểm hai xe gặp nhau.
Một nguồn sáng có công suất , phát ra ánh sáng tỏa ra đều theo mọi hướng mà mỗi phô tôn có năng lượng . Một người quan sát đứng cách nguồn sáng 300 km. Bỏ qua sự hấp thụ ánh sáng bởi khí quyển. Tính số phôtôn lọt vào mắt người quan sát trong mỗi giây. Coi bán kính con ngươi là 2 mm.
Một nguồn sáng có công suất , phát ra ánh sáng có bước sóng 0,6 µm tỏa ra đều theo mọi hướng. Hãy xác định khoảng cách xa nhất người còn trông thấy được nguồn sáng này. Biết rằng mắt còn cảm nhận được ánh sáng khi có ít nhất 100 phôtôn lọt vào mắt trong mỗi giây. Cho hằng số Plăng và tốc độ ánh sáng trong chân không . Coi đường kính con ngươi vào khoảng 4 mm. Bỏ qua sự hấp thụ ánh sáng bởi khí quyển.
Ánh sáng đơn sắc với bước sóng chiếu vuông góc vào một diện tích . Cho hằng số Plăng và tốc độ ánh sáng trong chân không . Nếu cường độ ánh sáng bằng thì số photon đập lên diện tích ấy trong một đơn vị thời gian là
Một nguồn bức xạ có công suất phát sáng phát ánh sáng đơn sắc có bước sóng . Cho hằng số Plăng và tốc độ ánh sáng trong chân không lần lượt là , . số phôtôn của nó phát ra trong 1 giây là:
Một ngọn đèn phát ánh sáng đơn sắc có công suất , trong 10 s phát ra được phôtôn. Cho hằng số Plăng và tốc độ ánh sáng trong chân không . Bức xạ này có bước sóng là
Một đèn Na chiếu sáng có công suất phát xạ . Bước sóng của ánh sáng vàng do đèn phát ra là . Hỏi trong 30 s, đèn phát ra bao nhiêu phôtôn? Cho hằng số plăng , tốc độ của ánh sáng toong chân không .
Một nguồn sáng có công suất , phát ra ánh sáng có bước sóng tỏa ra đều theo mọi hướng. Hãy xác định khoảng cách xa nhất người còn trông thấy được nguồn sáng này. Biết rằng mắt còn cảm nhận được ánh sáng khi có ít nhất 80 phôtôn lọt vào mắt trong mỗi giây. Cho hằng số Plăng và tốc độ ánh sáng trong chân không . Coi đường kính con ngươi vào khoảng 4 mm. Bỏ qua sự hấp thụ ánh sáng bởi khí quyển.
Ánh sáng đơn sắc với bước sóng chiếu vuông góc vào một diện tích . Cho hằng số Plăng và tốc độ ánh sáng trong chân không . Nếu cường độ ánh sáng bằng thì số photon đập lên điện tích ấy trong một đơn vị thời gian là
Dùng chùm tia laze có công suất P = 10 W để nấu chảy khối thép có khối lượng 1 kg. Nhiệt độ ban đầu của khối thép = 30°, nhiệt dung riêng của thép C = 448J/kg độ, nhiệt nóng chảy của thép L = 270 kJ/kg, điểm nóng chảy của thép = 1535°C. Coi rằng không bị mất nhiệt lượng ra môi trường. Thời gian làm nóng chảy hoàn toàn khối thép là:
Người ta dùng một laze hoạt động dưới chế độ liên tục để khoan một tấm thép. Công suất của chùm laze là P = 10 W. Đường kính của một chùm sáng là d = 1 mm. Bề dày của tấm thép là e = 2 mm. Nhiệt độ ban đầu là = 30°C. Khối lượng riêng của thép: = 7 800 kg/m3. Nhiệt dung riêng của thép: C = 448 J/kg.độ. Nhiệt nóng chảy riêng của thép: λ = 270 kJ/kg. Điểm nóng chảy của thép: = 1535°C. Bỏ qua mọi hao phí. Tính thời gian khoan thép.
Nước có nhiệt dung riêng c = 4,18 kJ/kg.độ, nhiệt hóa hơi L = 2260 kJ/kg, khối lượng riêng D = 1000 . Để làm bốc hơi hoàn toàn 1 nước ở nhiệt độ ban đầu 37°C trong khoảng thời gian 1s bằng laze thì laze này phải có công suất bằng:
Một laze có công suất 10 W làm bốc hơi một lượng nước ở 30°C. Biết rằng nhiệt dung riêng của nước là C = 4,18 kJ/kg.độ, nhiệt hóa hơi của nước L = 22601cJ/kg, khối lượng riêng của nước D = 1000. Thể tích nước bốc hơi được trong khoảng thời gian 1s là:
Dùng laze có công suất P = 10 W để làm dao mổ. Khi tia laze được chiếu vào vị trí cần mổ sẽ làm cho nước ở phần mô chỗ đó bốc hơi và mô bị cắt. Biết chùm laze có bán kính r = 0,1 mm và di chuyển với vận tốc v = 0,5cm/s trên bề mặt của mô mềm. Biết thể tích nước bốc hơi trong 1s là 3,5 . Chiều sâu cực đại của vết cắt là:
Trong y học, người ta dùng một laze phát ra chùm sáng có bước sóng λ để "đốt" các mô mềm. Biết rằng để đốt được phần mô mềm có thế tích 6 thì phần mô này cần hấp thụ hoàn toàn năng lượng của phôtôn của chùm laze trên. Coi năng trung bình để đốt hoàn toàn 1 mô là 2.53 J, Lấy ; . Giá trị của λ là?
Để đo khoảng cách từ Trái Đất lên Mặt Trăng người ta dùng một tia laze phát ra những xung ánh sáng có bước sóng 0,52 µm, chiếu về phía Mặt Trăng. Thời gian kéo dài mỗi xung là và công suất của chùm laze là 100000 MW. Biết tốc độ ánh sáng trong chân không và hằng số Plăng lần lượt là và . Số phôtôn chứa trong mỗi xung là:
Người ta dùng một loai laze có công suất P = 15 W để làm dao mô. Khi tia laze được chiếu vào vị trí cần mổ sẽ làm cho nước ở phần mô chỗ đó bốc hơi và mô bị cắt. Nhiệt độ cơ thể bệnh nhân là 37°C. Biết nhiệt dung riêng và nhiệt hoá hơi của nước lần lượt là C = 4,18kJ/kg.độ và L = 2260 kJ/kg. Tính trong 1s, thể tích nước mà tia laze có thể làm bốc hơi được là:
Một laze He − Ne phát ánh sáng có bước sóng 632,8 nm và có công suất đâu ra là 2,3 mW. Số phôtôn phát ra trong mỗi giờ là:
Hai bản kim loại phẳng có độ dài 30 cm đặt nằm ngang, song song cách nhau một khoảng 16 cm. Giữa hai bản tụ có một hiệu điện thế 4,55 (V). Hướng một chùm hẹp các electron quang điện có tốc độ theo phương ngang vào giữa hai bản tại điểm O cách đều hai bản. Khối lượng của electron là . Tính thời gian electron chuyển động trong tụ.
Một thanh kim loại MN dài 1 m trượt trên hai thanh ray song song đặt nằm ngang với vận tốc không đổi 2 m/s về phía tụ điện. Hai thanh ray đặt trong từ trường đều B = 1,5 T có phương thẳng đứng, có chiều hướng từ phía sau ra phía trước mặt phẳng hình vẽ. Hai thanh ray được nối với một ống dây và một tụ điện. Ống dây có hệ số tự cảm L = 5 mH, có điện trở R = 0,5 Ω. Tụ điện có điện dung C = 2 pF. Cho biết điện trở của hai thanh ray và thanh MN rất nhỏ. Chọn phương án đúng.
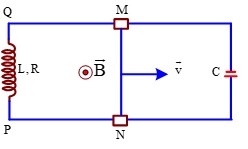
Một vật có khối lượng được thả rơi tự do xuống đất trong thời gian . Độ biến thiên động lượng của vật trong khoảng thời gian đó là bao nhiêu? Lấy .
Một vật có khối lượng rơi tự do xuống đất trong khoảng thời gian . Độ biến thiên động lượng của vật trong khoảng thời gian đó. Cho .
Một động cơ có công suất không đổi, công của động cơ thực hiện theo thời gian là đồ thị nào sau đây?

Đơn vị nào sau đây không phải là đơn vị của công suất?
Cho một máy bay lên thẳng có khối lượng sau thời gian 2 phút máy bay lên được độ cao là . Lấy . Tính công của động cơ khi chuyển động nhanh dần đều.
Một thang máy có khối lượng chuyển động nhanh dần đều lên cao với gia tốc . Tính công mà động cơ thang máy đã thực hiện trong đầu. Lấy .
Một đoàn tàu có khối lượng chuyển động nhanh dần đều từ địa điểm A đến địa điểm B cách nhau , khi đó vận tốc tăng từ (tại A) đến 20m/s (tại B). Tính công suất trung bình của đầu máy tàu trên đoạn đường AB. Cho biết hệ số ma sát là 0,005. Lấy .
Một đoàn tàu có khối lượng chuyển động nhanh dần đều đi qua hai địa điểm A và B cách nhau thì vận tốc tăng từ đến . Tính công suất trung bình của đầu máy trên đoạn đường AB. Cho biết hệ số ma sát 0,005. Lấy
Một ô tô, khối lượng là đang chuyển động đều trên con đường thẳng nằm ngang với vận tốc , với công suất của động cơ ô tô là . Sau đó ô tô tăng tốc, chuyển động nhanh dần đều và sau khi đi thêm được quãng đường vận tốc ô tô tăng lên đến . Tính công suất trung bình của động cơ ô tô trên quãng đường này và công suất tức thời của động cơ ô tô ở cuối quãng đường. Biết hệ số ma sát là 0,05. Lấy .
Muốn bơm nước từ một giếng sâu lên mặt đất người ta dùng một máy bơm có công suất 2 cv (mã lực), hiệu suất 50%. Tính lượng nước bơm được trong . Cho biết . Lấy .
Một vật khối lượng được kéo đều trên sàn bằng 1 lực hợp với phương ngang 1 góc α= 30° đi được . Nếu vật di chuyển quãng đường trên trong thời gian thì công suất của lực là bao nhiêu?
Một người nặng leo đều lên 1 cầu thang. Trong người đó leo được tính theo phương thẳng đứng. Cho . Công suất người đó thực hiện được tính theo Hp (mã lực ) là:
Công của trọng lực trong 2 giây cuối khi vật có khối lượng được thả rơi từ độ cao là bao nhiêu? Lấy .
Cho một vật có khối lượng rơi tự do. Tính công của trọng lực trong giây thứ tư. Lấy .
Cho một vật có khối lượng rơi tự do. Tính công của trọng lực trong giây thứ năm. Lấy .
Một học sinh của trung tâm bồi dưỡng kiến thức Hà Nội nâng tạ có khối lượng lên cao trong . Trong trường hợp học sinh đã hoạt động với công suất là bao nhiêu? Lấy
Cho một máy bay lên thẳng có khối lượng , sau thời gian máy bay lên được độ cao là . Tính công của động cơ khi chuyển động nhanh dần đều. Lấy
Cho một thang máy có khối lượng đi lên với gia tốc . Tìm công suất thang máy trong đầu tiên. Lấy
Khi 1 vật từ độ cao z, với cùng vận tốc đầu, bay xuống đất theo những con đường khác nhau (bỏ qua ma sát). Chọn câu sai.
Một học sinh của trung tâm bồi dưỡng kiến thức Hà Nội thả một vật rơi tự do có khối lượng từ tầng năm của trung tâm có độ cao so với mặt đất, bỏ qua ma sát với không khí. Tính thế năng của vật tại giây thứ hai so với mặt đất. Cho .
Một động cơ của xe máy có hiệu suất là 20 %. Sau một giờ hoạt động tiêu thụ hết xăng có năng suất toả nhiệt là . Công suất của động cơ xe máy là bao nhiêu?
Trong chuyển động thẳng chậm dần đều thì hợp lực tác dụng vào vật
Lực được biểu diễn bằng một vector cùng phương,
Một tên lửa khi chỉ chịu tác dụng của một lực không đổi theo chiều chuyển động sẽ chuyển động
Phát biểu nào sau đây là đúng?
Hình bên vẽ các lực tác dụng lên một chiếc xe đang chuyển động với vận tốc trên đường ngang. Nhận định nào sau đây sai?
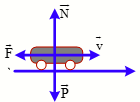
Một vật đang đứng yên trên mặt phẳng nằm ngang, bỏ qua ma sát giữa vật và mặt phẳng, thì được truyền 1 lực thì sau vật này đạt vận tốc . Nếu giữ nguyên hướng của lực mà tăng gấp 2 lần độ lớn lực vào vật đang đứng yên thì sau thì vận tốc của vật là bao nhiêu?
Một ôtô có khối lượng 1,5 tấn đang chuyển động với thì hãm phanh, chuyển động chậm dần đều. Biết lực hãm . Quãng đường và thời gian xe đi được cho đến khi dừng lại lần lượt là
Một vật có khối lượng 500g chuyển động nhanh dần đều với vận tốc ban đầu . Sau thời gian , nó đi được quãng đường . Biết vật luôn chịu tác dụng của lực kéo và lực cản . Tính độ lớn của lực kéo.
Một chiếc ô tô có khối lượng 5 tấn đang chạy thì bị hãm phanh chuyển động thẳng chậm dần đều. Sau thì dừng lại và đã đi được kể từ lúc vừa hãm phanh. Lập công thức vận tốc kể từ lúc vừa hãm phanh.
Một chiếc ô tô có khối lượng 5 tấn đang chạy thì bị hãm phanh chuyển động thẳng chậm dần đều. Sau 2,5s thì dừng lại và đã đi được 12m kể từ lúc vừa hãm phanh. Tìm lực hãm phanh.
Một vật có khối lượng bắt đầu chuyển động nhanh dần đều, nó đi được trong . Tính lực kéo, biết lực cản có độ lớn là .
Một vật có khối lượng bắt đầu chuyển động nhanh dần đều, nó đi được trong . Sau quãng đường ấy lực cản phải bằng bao nhiêu để vật có thể chuyển động thẳng đều?
Một vật đang đứng yên, được truyền 1 lực thì sau vật này tăng . Nếu giữ nguyên hướng của lực mà tăng gấp 2 lần độ lớn lực vào vật thì sau , vận tốc của vật là bao nhiêu?
Một ôtô có khối lượng đang chuyển động thẳng đều thì hãm phanh chuyển động chậm dần đều trong cuối cùng đi được . Hỏi lực hãm phanh tác dụng lên ôtô có độ lớn là bao nhiêu?
Lực tác dụng cùng phương chuyển động lên viên bi trong khoảng làm thay đổi vận tốc của viên bi từ 0 đến 5 cm/s. Nếu tác dụng lực cùng phương chuyển động lên viên bi trong khoảng thì vận tốc tại thời điểm cuối của viên bi là
Một đoàn tàu có khối lượng đang chạy với vận tốc thì bắt đầu tăng tốc. Sau khi đi được , vận tốc của nó lên tới . Biết lực kéo của đầu tàu trong cả giai đoạn tăng tốc là . Tìm lực cản chuyển động của đoàn tàu.
Một vật có khối lượng trượt xuống nhanh dần đều trên một con dốc dài , vận tốc tại đỉnh dốc bằng . Cho lực cản bằng . Góc nghiêng so với mặt phẳng nằm ngang là . Tìm gia tốc của vật, vận tốc tại chân dốc và thời gian trượt hết dốc.
Một vật có khối lượng trượt xuống nhanh dần đều trên một con dốc dài , vận tốc tại đỉnh dốc bằng . Cho lực cản bằng . Góc nghiêng . Sau khi rời khỏi mặt dốc, vật tiếp tục trượt trên mặt ngang với lực cản không đổi như trên. Hỏi sau bao lâu vật dừng lại, quãng đường vật đi được trên mặt ngang này?
Một quả bóng chày có khối lượng bay với vận tốc đến đập vuông góc với tường và bật ngược trở lại theo phương cũ với vận tốc . Thời gian va chạm là . Tính độ lớn lực do tường tác dụng vào quả bóng.
Người ta làm một thí nghiệm về sự va chạm giữa hai xe lăn trên mặt phẳng nằm ngang. Cho xe thứ nhất đang chuyển động với vận tốc . Xe thứ hai chuyển động với vận tốc đến va chạm vào phía sau xe một. Sau va chạm, hai xe cùng chuyển động với vận tốc là . So sánh khối lượng của hai xe.
Cho viên bi A chuyển động tới va chạm vào bi B đang đứng yên, sau va chạm bi A tiếp tục chuyển động theo phương cũ với , thời gian xảy ra va chạm là . Tính gia tốc của 2 viên bi, biết .
Cho hai vật chuyển động trên cùng một đường thẳng bỏ qua ma sát đến va chạm vào nhau với vận tốc lần lượt là ; . Sau va chạm cả hai bị bật ngược trở lại với vận tốc là ; . Biết vật một có khối lượng . Xác định khối lượng quả cầu hai.
Cho viên bi A chuyển động với vận tốctới va chạm vào bi B đang đứng yên, sau va chạm bi A tiếp tục chuyển động theo phương cũ với vận tốc , thời gian xảy ra va chạm là. Gia tốc của 2 viên bi lần lượt là bao nhiêu? Biết .
Một học sinh đá quả bóng có khối lượng bay với vận tốc đến đập coi như vuông góc với bức tường rồi bật trở lại theo phương cũ với vận tốc . Khoảng thời gian va chạm giữa bóng và tường bằng . Tính độ lớn lực tác dụng của tường lên quả bóng?
Một vật dao động điều hòa với biên độ A và chu kỳ T. Trong khoảng thời gian , quãng đường lớn nhất mà vật đi được là
Một vật dao động điều hòa với biên độ A và chu kỳ T. Trong khoảng thời gian 2T/3, quãng đường lớn nhất (Smax) mà vật đi được là
Một vật đao động điều hòa với phương trình cm. Quãng đường lớn nhất vật đi được trong khoảng thời gian 1,5 s là (lấy gần đúng)
Một vật dao động điều hòa với phương trình cm. Tính quãng đường lớn nhất mà vật đi được trong khoảng thời gian 7T/12 (lấy gần đúng).
Một vật dao động điều hòa với chu kỳ 2 s, biên độ 4 cm. Tìm quãng đường dài nhất vật đi được trong khoảng thời gian 5/3 s
Cho một vật có khối lượng đang đứng yên trên mặt phẳng nằm ngang, tác dụng một lực là có phương hợp với phương ngang một góc . Sau khi đi được thì đạt được vận tốc . Ban đầu bỏ qua ma sát, xác định khối lượng của vật.
Cho một vật có khối lượng 2 kg đang đứng yên trên mặt phẳng nằm ngang, tác dụng một lực là có phương hợp với phương ngang một góc . Giả sử hệ số ma sát giữa vật và sàn là 0,1 thì sau khi đi được quãng đường thì vận tốc của vật là bao nhiêu? Cho
Cho một vật đứng yên có khối lượng đặt trên một sàn nhà. Một người tác dụng một lực là kéo vật theo phương ngang, hệ số ma sát giữa vật và sàn nhà là . Cho . Sau khi đi được quãng đường 4,5m thì vật có vận tốc là bao nhiêu, thời gian đi hết quãng đường đó?
Cho một vật có khối lượng đặt trên một sàn nhà. Một người tác dụng một lực là để kéo vật, hệ số ma sát giữa vật và sàn nhà là . Cho . Biết lực kéo hợp với phương chuyển động một góc thì vận tốc của vật sau 5 s là
Một vật dao động điều hòa với biên độ A và chu kỳ T. Trong khoảng thời gian , quãng đường nhỏ nhất mà vật đi được là
Một vật dao động điều hòa với phương trình cm. Quãng đường nhỏ nhất vật đi được trong khoảng thời gian 2/3 chu kỳ là (lấy gần đúng)
Một vật dao động điều hòa với phương cm. Quãng đường nhỏ nhất vật đi được trong khoảng thời gian là
Một vật dao động điều hòa với phương trình cm. Quãng đường nhỏ nhất vật đi được trong khoảng thời gian 1,5 s là (lấy gần đúng)
Một vật dao động điều hòa với biên độ A và chu kỳ T. Trong khoảng thời gian , quãng đường nhỏ nhất mà vật đi được là
Vật có đang đứng yên. Tác dụng một lực hợp với phương chuyển động một góc là . Sau khi chuyển động , vật đi được một quãng đường là , cho . Hệ số ma sát trượt giữa vật và mặt sàn là bao nhiêu?
Một vật đặt ở chân mặt phẳng nghiêng một góc so với phương nằm ngang. Hệ số ma sát trượt giữa vật và mặt phẳng nghiêng là . Vật được truyền một vận tốc ban đầu theo phương song song với mặt phẳng nghiêng và hướng lên phía trên. Sau bao lâu vật lên tới vị trí cao nhất?
Cho một mặt phẳng nghiêng một góc . Đặt một vật có khối lượng rồi tác dụng một lực là song song với mặt phẳng nghiêng làm cho vật chuyển động đi lên nhanh dần đều, biết hệ số ma sát giữa vật và mặt phẳng nghiêng là . Xác định quãng đường vật đi được trong giây thứ 2.
Cho một vật có khối lượng m đang chuyển động với vận tốc trên mặt phẳng nằm ngang thì trượt lên dốc. Biết dốc dài , cao và hệ số ma sát giữa vật và dốc là . Lấy . Vật có lên hết dốc không? Nếu có tính vận tốc của vật ở đỉnh dốc và thời gian lên hết dốc.
Cho một dốc con dài , cao . Cho một vật có khối lượng m đang chuyển động thẳng đều với vận tốc trên mặt phẳng nằm ngang thì lên dốc và vật đi đến đỉnh dốc thì ngừng lại. Biết hệ số ma sát giữa vật và dốc là . Lấy . Ngay sau đó vật trượt xuống, vận tốc của nó khi xuống đến chân dốc và tìm thời gian chuyển động kể từ khi bắt đầu lên dốc cho đến khi xuống đến chân dốc lần lượt là
Một vật trượt từ đỉnh mặt phẳng nghiêng dài , cao . Bỏ qua ma sát trên mặt phẳng nghiêng. Hỏi sau khi đến chân mặt phẳng nghiêng, vật tiếp tục chuyển động trên mặt phẳng ngang một quãng đường bao nhiêu và trong thời gian bao lâu? Biết hệ số ma sát giữa vật và mặt phẳng ngang là 0,1. Lấy
Một vật trượt từ đỉnh một dốc phẳng dài , chiều cao xuống không vận tốc đầu, hệ số ma sát giữa vật và mặt phẳng nghiêng là . Xác định thời gian vật trượt hết chiều dài của dốc và vận tốc của vật đó ở cuối chân dốc.
Một vật khối lượng đang đứng yên trên mặt phẳng nằm ngang. Tác dụng một lực có độ lớn là và hợp với phương ngang một góc cho và biết hệ số ma sát giữa sàn và vật là . Sau vật đi được quãng đường là bao nhiêu?
Một người đang chơi ở đỉnh tòa nhà cao cầm một vật có khối lượng m ném theo phương ngang với vận tốc ban đầu là xuống đất, bỏ qua lực cản của không khí. Cho . Viết phương trình quỹ đạo của vật, khoảng thời gian vật chạm đất và khoảng cách từ nhà đến vị trí rơi.
Một người đang chơi ở đỉnh tòa nhà cao , cầm một vật có khối lượng ném theo phương ngang với vận tốc ban đầu là xuống đất, bỏ qua lực cản của không khí. Cho . Gọi M là điểm bất kỳ trên quỹ đạo rơi của vật mà tại đó vec tơ vận tốc hợp với phương thẳng đứng một góc . Tính độ cao của vật khi đó.
Một người đứng ở độ cao 80m ném một vật theo phương ngang thì vật phải có vận tốc ban đầu là bao nhiêu để ngay lúc chạm đất có , bỏ qua lực cản của không khí. Tính vận tốc lúc ném và tầm ném xa của vật khi chạm đất.
Một quả cầu được ném theo phương ngang từ độ cao . Sau khi chuyển động 3s, vận tốc quả cầu hợp với phương ngang một góc . Tính vận tốc ban đầu của quả cầu.
Một quả cầu được ném theo phương ngang từ độ cao 80m. Sau khi chuyển động 3s, vận tốc quả cầu hợp với phương ngang một góc . Thời gian chuyển động của vật, vị trí tiếp đất, vận tốc của vật là bao nhiêu khi tiếp đất?
Một máy bay bay ngang với vận tốc ở độ cao muốn thả bom trúng một tàu chiến đang chuyển động đều với vận tốc trong cùng mặt phẳng thẳng đứng với máy bay. Hỏi máy bay phải thả bom khi nó cách tàu chiến theo phương ngang một đoạn xa là bao nhiêu để bom rơi trúng tàu chiến? Biết máy bay và tàu chuyển động cùng chiều.
Một máy bay ném bom đang bay theo phương ngang ở độ cao với vận tốc . Hỏi viên phi công phải thả bom từ xa cách mục tiêu bao nhiêu để bom rơi trúng mục tiêu? Lấy .
Từ sân thượng cao 80m một người đã ném một hòn đá theo phương ngang với . Lấy . Khi vận tốc của viên đá hợp với phương thẳng đứng một góc thì vật có độ cao bằng bao nhiêu, độ lớn vận tốc khi đó?
Một vật được ném theo phương ngang từ độ cao , có tầm ném xa là . Bỏ qua sức cản của không khí. Lấy . Tính vận tốc ban đầu và vận tốc của vật lúc chạm đất.
Một vật dao động điều hòa với phương trình cm. Tốc độ trung bình nhỏ nhất vật đi được trong khoảng thời gian 1,5 s là (lấy gần đúng)
Một vật dao động điều hòa với biên độ A và chu kỳ T. Trong khoảng thời gian , tốc độ trung bình nhỏ nhất mà vật đi được là
Một chất điểm dao động điều hoà dọc trục Ox quanh VTCB O với biên độ A và chu kì T. Theo phương trình với x tính bằng cm và t tính bằng s. Hãy xác định tốc độ trung bình nhỏ nhất vật đi được trong .
Một chất điểm dao động điều hoà dọc trục Ox quanh VTCB O với biên độ A và chu kì T. Trong khoảng thời gian tốc độ trung bình lớn nhất của chất điểm là
Một vật dao động điều hòa với biên độ A và chu kỳ T. Trong khoảng thời gian , tốc độ trung bình lớn nhất của vật là
Một vật dao động điều hòa với phương trình cm. Tính tốc độ trung bình lớn nhất mà vật đi được trong khoảng thời gian 7T/12 (lấy gần đúng).
Một con lắc lò xo có vật nặng với khối lượng và lò xo có độ cứng dao động với biên độ 2 cm. Thời gian mà vật có vận tốc không nhỏ hơn trong mỗi chu kì là bao nhiêu?
Một con lắc lò xo nằm ngang lý tưởng dao động với biên độ 2 cm. Lò xo có độ cứng của lò xo 100 N/m, vật nặng có khối lượng là 400 g. Khoảng thời gian ngắn nhất giữa 2 lần liên tiếp vật đi qua vị trí lò xo bị nén 2 cm là 1 giây. Hỏi quãng đường lớn nhất vật đi được trong 5 giây là bao nhiêu? Cho
Một con lắc lò xo dao điều hòa theo phương thẳng đứng với phương trình dao động . Quãng đường con lắc lò xo có chất điểm mà điểm đó đi được từ đếns là
Một con lắc lò xo dao động điều hòa theo phương ngang với phương trình dao động . Quãng đường con lắc lò xo có chất điểm đó đi được từ đến s là
Một con lắc lò xo có độ cứng , đầu trên cố định còn đầu dưới gắn vật nặng , Cho vật m dao động điều hòa theo phương thẳng đứng thì thấy thời gian lò xo nén trong chu kỳ là 0,1s. Cho , biên độ dao động của vật là
Một con lắc lò xo dao động điều hòa theo phương thẳng đứng, khi con lắc ở vị trí cân bằng lò xo dãn 9 cm. Thời gian con lắc bị nén trong chu kỳ là 0,1s. Lấy . Biên độ dao động của vật là
Một lò xo khối lượng không đáng kể độ cứng . Một đầu treo vào một điểm cố định, đầu còn lại treo một vật nặng khối lượng 500g. Từ vị trí cân bằng kéo vật xuống dưới theo phương thẳng đứng một đoạn 10cm rồi buông nhẹ cho vật dao động điều hòa. Lấy . Xác định thời gian mà lò xo bị nén và bị dãn trong một chu kỳ
Một con lắc lò xo treo thẳng đứng, từ vị trí cân bằng kéo vật xuống dưới trục của lò xo với vị trí lò dãn 7,5 cm rồi thả nhẹ cho nó dao động điều hòa, sau một khoảng thời gian ngắn nhất (s) thì gia tốc của vật bằng 0,5 gia tốc ban đầu. Lấy gia tốc trọng trường . Thời gian mà lò xo bị nén trong một chu kì là
Một con lắc đơn chiều dài và gắn vào vật có khối lượng m dao động điều hòa trên Ox với biên độ 10cm, chu kì 2s. Mốc thế năng ở vị trí cân bằng. Tốc độ trung bình của vật trong khoảng thời gian ngắn nhất khi chất điểm đi từ vị trí có động năng 3 lần thế năng đến vị trí có động năng bằng thế năng là
Một con lắc lò xo dao động điều hòa với chu kì T, để chu kì dao động tăng lên 5% thì khối lượng của vật phải
Một vật dao động điều hòa với phương trình . Tốc độ trung bình của vật từ thời điểm 2/3s đến 37/12s là
Một vật dao động điều hòa trên trục Ox đi từ vị trí P có li độ đến vị trí Q có li độ . Vật tiếp tục đi thêm 21 cm nữa thì quay lại P và kết thúc một chu kì. Biên độ dao động của vật không thể nhận giá trị nào sau đây?
Một xe chuyển động nhanh dần đều đi trên hai đoạn đường liên tiếp bằng nhau 100 m, lần lượt trong 5s và 3,5s. Tính gia tốc của xe.
Vệ tinh A của Việt Nam được phóng lên quỹ đạo ngày 19/4/2008. Sau khi ổn định, vệ tinh chuyển động tròn đều với v = 2,21 km/h ở độ cao 2400 km so với mặt đất. Bán kính Trái Đất là 6389 km. Tính tốc độ góc, chu kì, tần số của vệ tinh.
Một người thả vật rơi tự do, vật chạm đất có , .
a) Tìm độ cao thả vật.
b) Vận tốc vật khi rơi được 15 m.
c) Độ cao của vật sau khi đi được .
Thả một hòn đá từ độ cao h xuống đất và hòn đá rơi trong 1s. Nếu thả hòn đá từ độ cao h’= 4h thì thời gian rơi là?
Một vật được thả rơi tự do từ một độ cao so với mặt đất thì thời gian rơi là 5 s. Nếu vật này được thả rơi tự do từ cùng một độ cao nhưng ở Mặt Trăng có gia tốc rơi tự do là thì thời gian rơi sẽ là
Một xe lửa dừng lại hẳn sau 20s kể từ lúc bắt đầu hãm phanh. Trong thời gian đó xe chạy được 120 m. Tính vận tốc của xe lúc bắt đầu hãm phanh và gia tốc của xe.
Một chiếc xe lửa chuyển động trên đoạn thẳng qua điểm A với , . Tại B cách A 100 m. Tìm vận tốc của xe tại điểm B.
Một xe chạy trong 5 giờ, 2 giờ đầu xe chạy với tốc độ trung bình 60 km/h, 3 giờ sau xe chạy với tốc độ trung bình 40 km/h. Tính tốc độ trung bình của xe trong suốt thời gian chuyển động.
Phương trình cơ bản của một vật chuyển động: . Hãy xác định tính chất chuyển động của vật.
Từ phương trình chuyển động: . Tính chất của chuyển động là?
Một vật dao động điều hoà theo phương trình . Tỉ số động năng và cơ năng của vật tại độ là
Một vật dao động điều hòa theo phương trình (cm) . Thời gian vật đi được quãng đường 22,5 cm kể từ lúc bắt đầu chuyển động (t = 0) là
Con lắc đơn có chiều dài 24 cm, được treo vào trần một toa xe lửa. Con lắc sẽ dao động cưỡng bức mỗi khi bánh xe của toa xe gặp chỗ nối giữa hai thanh ray. Chiều dài mỗi thanh ray là 10,5 m. Lấy . Con lắc dao động mạnh nhất khi xe lửa chạy thẳng đều với vận tốc xấp xỉ bằng
Một vật dao động điều hòa với tần số là f thì có động năng biến thiên tuần hoàn với chu kỳ 0,1s. Giá trị tần số f của dao động là
Chất điểm dao động điều hòa với chu kì T. Trong một chu kì, khoảng thời gian tốc độ của chất điểm có giá trị vượt quá là
Trong dao động điều hòa, vận tốc biến đổi
Một chất điểm dao động điều hòa trên trục Ox theo phương trình . Tại thời điểm vận tốc của chất điểm bằng
Con lắc lò xo dao động thẳng đứng với cơ năng là W = 0,072 J. Vật gắn vào lò xo có khối lượng m = 100 g . Lấy . Lúc vật m dao động qua vị trí lò xo không biến dạng thì động năng của nó là 47 mJ. Khi con lắc lò xo đứng yên thì độ giãn của lò xo là
Một con lắc lò xo gồm một lò xo nhẹ có độ cứng k = 100 và vật nhỏ có khối lượng m = 100 g. Con lắc dao động điều hòa theo phương ngang với chu kì T và sau khi thực hiện 50 dao động thì đi được quãng đường là 16 m. Biết ở thời điểm t vật có li độ 5 cm. Vào thời điểm t + vật qua vị trí có độ lớn li độ gần nhất với giá trị nào sau đây
Con lắc lò xo có độ cứng là 80 , dao động điều hòa với biên độ 5 cm. Động năng của con lắc khi qua vị trí có li độ x = -3 cm là
Một vật dao động điều hòa trên đoạn thẳng dài 8 cm với chu kì . Chọn gốc thời gian là lúc vật đi qua theo chiều âm. Phương trình dao động của vật là
Một ô tô chuyển động thẳng nhanh dần đều với vận tốc ban đầu là 18km/h. Trong giây thứ 6 xe đi được quãng đường 21,5m. Tính gia tốc của xe. Tính quãng đường xe đi trong 20s đầu tiên.
Một ô tô chuyển động thẳng nhanh dần đều với vận tốc đầu là 54 km/h. Trong giây thứ 4 vật đi được quãng đường 22 m. Tính gia tốc của ô tô.
Một vật chuyển động thẳng nhanh dần đều từ trạng thái đứng yên và đi được đoạn đường S trong thời gian 4s. Xác định thời gian vật được đoạn đường cuối.
Một xe ô tô chuyển động thẳng nhanh dần đều với vận tốc đầu 18km/h. Trong giây thứ tư kể từ lúc bắt đầu chuyển động nhanh dần, xe đi được 12m. Hãy tính gia tốc của vật và quãng đường đi được sau 10s.
Một xe chuyển động nhanh dần đều với vận tốc đầu 18km/h. Trong giây thứ 5 xe đi được 14m. Tính gia tốc của xe.
Một xe đang chuyển động thẳng đều với vận tốc . Xe đột ngột hãm phanh để dừng ngay trước vạch đèn đỏ. Biết khoảng cách từ xe đến vạch là . Hãy tính thời gian xe chuyển động kể từ lúc hãm phanh đến lúc dừng lại. Giả sử xe chuyển động chậm dần đều.
Xe đang chuyển động đều trên đường thì gặp một đoạn bục giảm tốc. Sau khi rời khỏi bục giảm tốc, xe giảm so với vận tốc ban đầu. Biết đoạn bục giảm tốc dài trong 0,5 giây. Tính vận tốc ban đầu của xe.
Một xe đang đứng yên thì bắt đầu chuyển động. Sau 5 giây, vật đạt vận tốc . Hỏi quãng đường vật đi được khi đạt được vận tốc .
Một xe chuyển động từ chân dốc một mặt phẳng nghiêng với vận tốc , sau khi đến đỉnh dốc, vật có vận tốc . Biết quá trình này mất thời gian 10 giây. Tính quãng đường vật đi được.
Một chiếc thuyền đang đứng yên bắt đầu chuyển động. Nếu thuyền không khởi động động cơ thì sau 5 giây, thuyền trôi được quãng đường 1 m. Hỏi nếu thuyền khởi chạy với gia tốc là , thì vận tốc của thuyền khi đi được quãng đường 10m khi đi xuôi dòng?
Một vật dao động điều hòa với phương trình li độ . Lúc vật
Một vật nhỏ dao động điều hòa với biên độ . Quãng đường nhỏ nhất mà vật đi được trong là . Tốc độ lớn nhất của vật gần bằng
Một con lắc đơn dao động điều hòa có biên độ dài tại nơi có gia tốc trọng trường Biết chiều dài của dây dài . Hãy viết phương trình dao động. Biết lúc vật đi qua vị trí cân bằng theo chiều dương ().
Nếu giữ biên độ dao động không đổi và cho khối lượng quả cầu của con lắc lò xo tăng lên hai lần thì
Một con lắc lò xo treo thẳng đứng. Khi vật đứng yên lò xo giãn 10 cm. Lấy . Chu kì riêng của con lắc là
Một vật dao động điều hòa trên trục Ox quanh vị trí cân bằng là gốc O. Tại thời điểm ban đầu vật đi qua vị trí cân bằng theo chiều dương, đến thời điểm = s thì vật vẫn chưa đổi chiều và động năng vật giảm đi 4 lần so với lúc đầu, đến thời điểm s vật đi quãng đường 9 cm. Tốc độ ban đầu của vật bằng
Một chất điểm dao động điều hòa với phương trình gia tốc . Lấy = 10. Xác định biên độ dao động của vật.
Chọn câu sai. Trong dao động điều hòa thì li độ, vận tốc và gia tốc là những đại lượng biến đổi theo hàm sin hoặc cosin theo thời gian t và
Khi một con lắc lò xo dao động theo phương ngang với biên độ 4 cm. Nếu chọn mốc thế năng tại vị trí cân bằng thì tại vị trí thế năng bằng 4 mJ, lực đàn hồi có độ lớn 0,4 N. Năng lượng dao động của hệ là
Một vật dao động với phương trình . Hãy xác định số dao động vật thực hiện trong 1s là
Một vật đang chuyển động đều sau đó tăng tốc dần. Tính gia tốc của xe biết rằng trước khi tăng tốc, cứ 12 m xe đi trong 2 s và sau khi tăng tốc đến vận tốc vật được quãng đường là .
Cho một vật đang chuyển động thẳng đều có đồ thị chuyển động như sau. Với t được tính bằng giờ và x được tính bằng km.

Hãy xác định phương trình chuyển động của vật.
Cho đồ thị như hình vẽ. Dựa vào đồ thị, hãy lập phương trình chuyển động của hai xe.
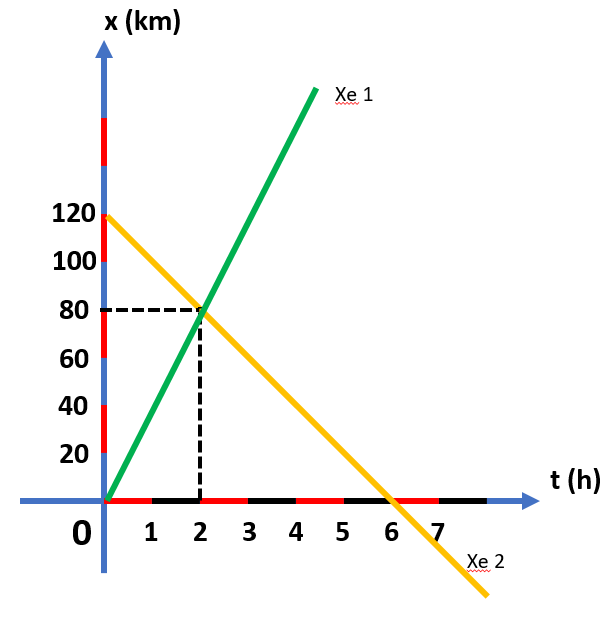
Một người đi xe đạp từ A và một người đi bộ từ B cùng lúc và cùng theo hướng AB. Người đi xe đạp đi với vận tốc v = 12 km/h, người đi bộ đi với v = 5 km/h. Khoảng cách AB = 14km. Chọn gốc tọa độ tại A, chiều dương từ A đến B. Chọn đáp án đúng. Đồ thị tọa độ - thời gian của hai xe là
Cho đồ thị tọa độ - thời gian của vật chuyển động thẳng đều. Câu nào sau đây không đúng khi nói về tính chất chuyển động của vật?
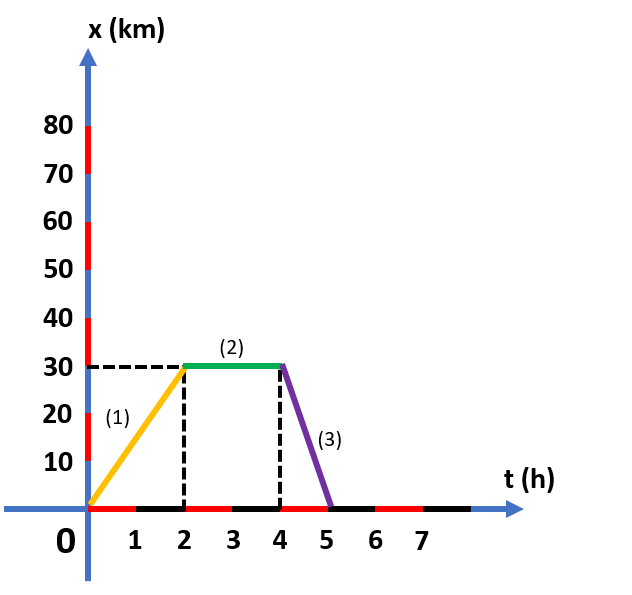
Chọn câu trả lời đúng nhất. Trong các đồ thị sau đây, đồ thị nào có dạng của vật đang chuyển động thẳng đều?
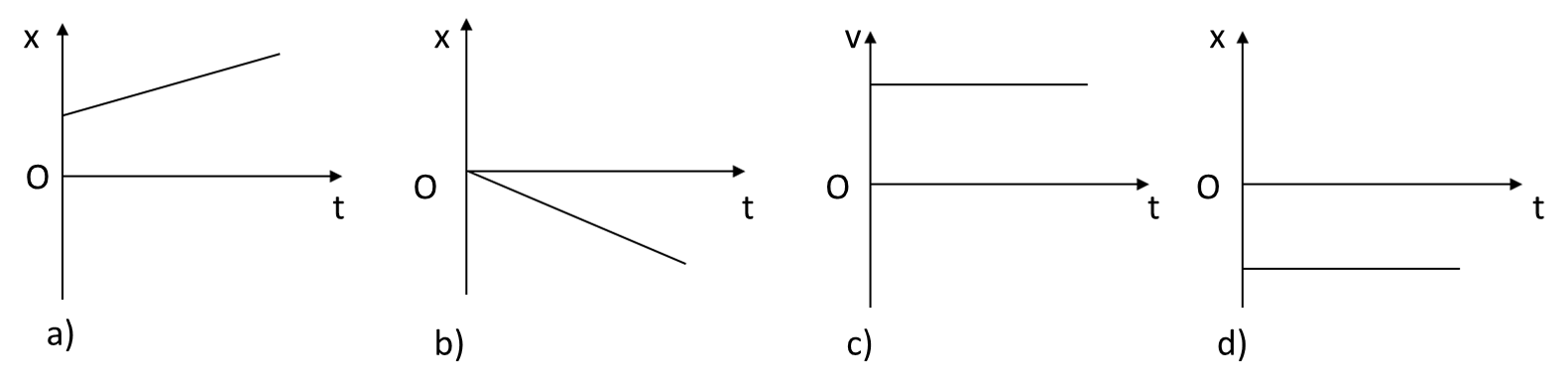
Cho đồ thị tọa độ - thời gian của hai xe như hình vẽ. Đặc điểm chuyển động của hai xe là
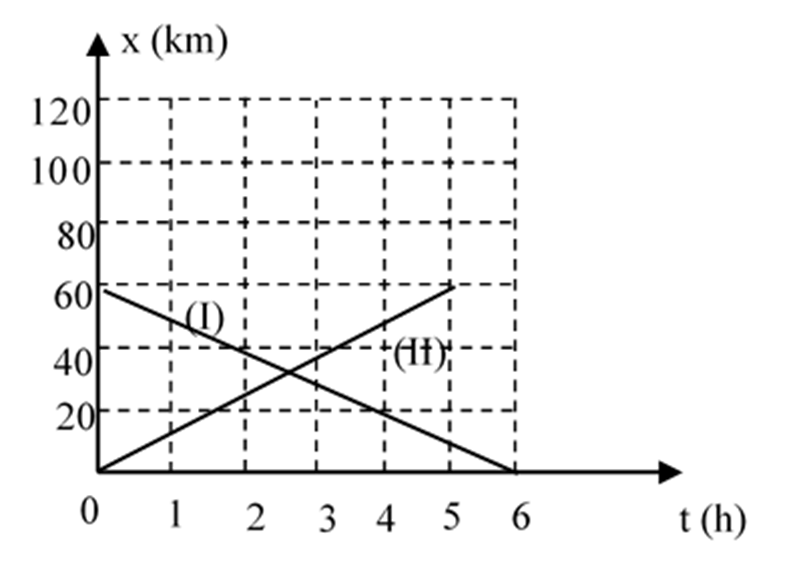
Gia tốc là một đại lượng
Trong chuyển động thẳng chậm dần đều, gia tốc
Vectơ gia tốc của chuyển động thẳng biến đổi đều.
Một vật chuyển động thẳng chậm dần đều có vận tốc ban đầu , gia tốc có động lớn không đổi theo thời gian. Phương trình vận tốc có dạng: . Vật này có:
Chọn ý sai. Chuyển động thẳng nhanh dần đều có:
Chuyển động thẳng chậm dần đều có
Chọn ý sai. Khi một chất điểm chuyển động thẳng biến đổi đều thì nó có:
Chọn phát biểu đúng
Chọn phát biểu sai:
Để đặc trưng cho chuyển động về sự nhanh, chậm và về phương chiều, người ta đưa ra khái niệm
Nhận xét nào sau đây là không đúng về một chất điểm chuyển động thẳng theo một chiều với gia tốc ?
Trong công thức tính vận tốc của chuyển động thẳng nhanh dần đều , thì
Trong công thức tính vận tốc của chuyển động thẳng nhanh dần đều thì:
Điều khẳng định nào dưới đây chỉ đúng cho chuyển động thẳng nhanh dần đều?
Nhận xét nào sau đây không đúng với một chất điểm chuyển động thẳng theo một chiều với gia tốc
Phương trình chuyển động của một vật trên trục Ox có dạng: . Trong đó t tính bằng giây, x tính bằng mét. Vật này chuyển động
Công thức tính quãng đường đi được của chuyển động thẳng nhanh dần đều là
Phương trình của chuyển động thẳng chậm dần đều là
Phương trình chuyển động của một chất điểm dọc theo trục Ox là (x tính bằng m ; t tính bằng s) thì chất điểm chuyển động
Phương trình nào sau đây là phương trình tọa độ của một vật chuyển động thẳng chậm dần đều dọc theo trục Ox?
Phương trình chuyển động của vật có dạng: (m; s). Biểu thức vận tốc tức thời của vật theo thời gian là:
Một vật chuyển động thẳng biến đổi đều có: Khi thì và còn khi thì . Viết phương trình chuyển động của vật.
Một vật chuyển động thẳng biến đổi đều có: Khi thì và còn Khi thì . Xác định thời điểm mà vật đổi chiều chuyển động và vị trí của vật lúc này.
Cho một vật chuyển động thẳng biến đổi đều có phương trình: . Vận tốc của vật ở thời điểm t = 10 s.
Cho một vật chuyển động thẳng biến đổi đều có phương trình: . Toạ độ của vật khi nó có v = 4 m/s.
Cho một vật chuyển động thẳng biến đổi đều có phương trình chuyển động là ( m;s). Xác định vận tốc và quãng đường của chuyển động sau 2s là bao nhiêu?
Một vật chuyển động thẳng biến đổi đều với phương trình chuyển động thẳng là: (m;s). Tính quãng đường vật đi được trong khoảng thời gian từ đến và vận tốc trung bình trong khoảng thời gian này.
Một vật chuyển động thẳng biến đổi đều với phương trình chuyển động thẳng là: (m;s). Tính vận tốc của vật lúc t = 6s.
Đồ thị vận tốc theo thời gian của chuyển động thẳng như hình vẽ. Chuyển động thẳng nhanh dần đều là đoạn nào?
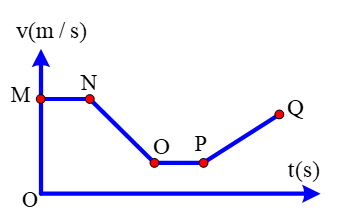
Đồ thị vận tốc theo thời gian của một xe máy chuyển động trên một đường thẳng được biểu diễn như hình vẽ. Trong khoảng thời gian nào, xe máy chuyển động chậm dần đều?
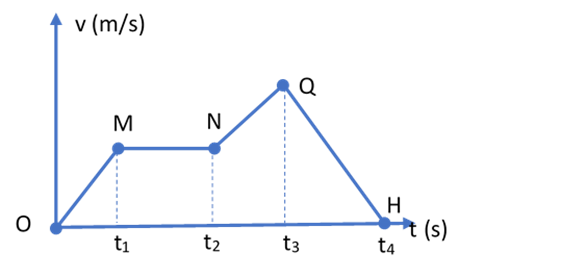
Đồ thị vận tốc − thời gian của một vật chuyển động được biểu diễn như hình vẽ. Gọi lần lượt là gia tốc của vật trong các giai đoạn tương ứng là từ t = 0 đến = 20 s; từ = 20 s đến = 60 s; từ = 60 s đến = 80 s. Giá trị của lần lượt là

Đồ thị vận tốc − thời gian của một vật chuyển động được biểu diễn như hình vẽ. Quãng đường vật đi được từ thời điểm t = 0, đến thời điểm t = 60 s là
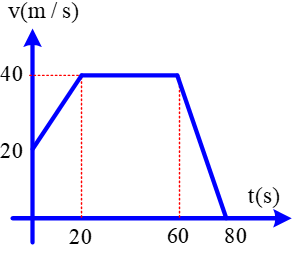
Một ôtô bắt đầu chuyển động thẳng nhanh dần đều. Trong giây thứ 6 xe đi được quãng đường 11m. Tính gia tốc của xe.
Một ôtô bắt đầu chuyển động thẳng nhanh dần đều. Trong giây thứ 6 xe đi được quãng đường 11m. Tính quãng đường xe đi trong 20s đầu tiên.
Một xe chuyển động nhanh dần đều với vận tốc đầu 18km/h. Trong giây thứ 5 xe đi được 14m. Tính gia tốc của xe.
Một xe chuyển động nhanh dần đều với vận tốc đầu 18km/h. Trong giây thứ 5 xe đi được 14m. Tính quãng đường đi được trong giây thứ 10.
Một bắt đầu vật chuyển động nhanh dần đều trong 10s với gia tốc của vật 2 . Quãng đường vật đi được trong 2s cuối cùng là bao nhiêu?
Một vật chuyển động thẳng biến đổi đều không vận tốc đầu và đi được quãng đường S mất 3s. Tìm thời gian vật đi được 8/9 đoạn đường cuối.
Một ô tô đang đi với v = 54 km/h bỗng người lái xe thấy có ổ gà trước mắt cách xe 54 m. Người ấy phanh gấp và xe đến ổ gà thì dừng lại. Tính gia tốc và thời gian hãm phanh.
Cho một máng nghiêng, lấy một viên bi lăn nhanh dần đều từ đỉnh một máng với không vận tốc ban đầu, bỏ qua ma sát giữa vật và máng, biết viên bi lăn với gia tốc 1 . Sau bao lâu viên bi đạt vận tốc 2 m/s.
Cho một máng nghiêng, lấy một viên bi lăn nhanh dần đều từ đỉnh một máng với không vận tốc ban đầu, bỏ qua ma sát giữa vật và máng, biết viên bi lăn với gia tốc 1 . Biết vận tốc khi chạm đất 4 m/s. Tính chiều dài máng và thời gian viên bi chạm đất.
Một người đi xe đạp chuyển động nhanh dần đều đi được = 24m, = 64m trong 2 khoảng thời gian liên tiếp bằng nhau là 4s. Xác định vận tốc ban đầu và gia tốc của xe đạp.
Một ô tô đang chạy với vận tốc 15m/s trên đoạn đường thẳng thì người lái xe tăng ga và ô tô chuyển động nhanh dần đều. Sau 10s xe đạt đến vận tốc 20m/s. Tính gia tốc và vận tốc của xe ôtô sau 20s kể từ lúc tăng ga?
Một xe chuyển động thẳng nhanh dần đều đi trên hai đoạn đường liên tiếp bằng nhau 100m, lần lượt trong 5s và 3s. Tính gia tốc của xe.
Thả một viên đá rơi từ miệng một cái hang sâu xuống đáy. Sau 4s kể từ lúc bắt đầu thả thì nghe được tiếng viên đá chạm vào đáy. Tính chiều sâu của hang. Biết vận tốc truyền âm trong không khí là 330 m/s. Lấy .
Một hòn đá rơi từ miệng một giếng cạn đến đáy giếng mất 3s. Tính độ sâu của giếng và vận tốc hòn đá khi chạm đáy giếng, lấy .
Một hòn đá được thả rơi từ miệng một cái giếng nhỏ có độ sâu là 320 m. Sau bao lâu từ lúc thả rơi, người ta nghe thấy tiếng hòn đá đập vào đáy giếng. Cho biết tốc độ truyền âm trong không khí không đổi và bằng 320 m/s, lấy
Thả một hòn đá xuống đáy một cái giếng cạn thì sau 0,1 s nghe thấy âm thanh phát ra từ đáy giếng. Tính độ sâu của giếng biết vận tốc truyền âm trong không khí là 340 m/s. Lấy .
Đồ thị vận tốc – thời gian của một tàu hỏa đang chuyển động thẳng có dạng như hình bên. Thời điểm t = 0 là lúc tàu đi qua sân ga. Vận tốc của tàu sau khi rời sân ga được 80 m là

Đồ thị vận tốc – thời gian của một vật chuyển động thẳng ở hình dưới. Quãng đường vật đã đi được sau 30s là

Đồ thị gia tốc – thời gian của một vật chuyển động từ trạng thái nghỉ ở hình bên. Quãng đường vật đi được sau 2 s đầu tiên là

Gọi M, N, I là các điểm trên một lò xo nhẹ, được treo thẳng đứng ở điểm O cố định. Khi lò xo có chiều dài tự nhiên thì OM = MN = NI = 10 cm. Gắn vật nhỏ vào đầu dưới I của lò xo và kích thích để vật dao động điều hòa theo phương thẳng đứng. Trong quá trình dao động, tỉ số độ lớn lực kéo lớn nhất và độ lớn lực kéo nhỏ nhất tác dụng lên O bằng 3; lò xo giãn đều; khoảng cách lớn nhất giữa M và N là 12 cm. Lấy . Vật dao động với tần số là
Một electron chuyển động cùng hướng với đường sức của một điện trường đều rất rộng có cường độ 364 V/m. Electron xuất phát từ điểm M với độ lớn vận tốc 3,2. m/s. Cho biết điện tích và khối lượng của electron lần lượt là: -1,6. C và m = 9,1. kg. Thời gian kể từ lúc xuất phát đến lúc electron trở về điểm M là
Một điện tích điểm đặt tại O, một thiết bị đo độ lớn cường độ điện trường chuyển động thẳng từ M hướng đến O theo hai giai đoạn với vận tốc ban đầu bằng không và gia tốc có độ lớn 7,5 cho đến khi dừng lại tại điểm N. Biết NO = 15 cm và số chỉ thiết bị đo tại N lớn hơn tại M là 64 lần. Thời gian thiết bị đó chuyển động từ M đến N có giá trị gần giá trị nào nhất sau đây?
Từ điểm A bắt đầu thả rơi tự do một điện tích điểm, khi chạm đất tại B nó đứng yên luôn. Tại C, ở khoảng giữa A và B (nhưng không thuộc AB), có một máy M đo độ lớn cường độ điện trường, C cách AB là 0,6 m. Biết khoảng thời gian từ khi thả điện tích đến khi máy M thu có số chỉ cực đại, lớn hơn 0,2 s so với khoảng thời gian từ đó đến khi máy M số chỉ không đổi, đồng thời quãng đường sau nhiều hơn quãng đường trước là 0,2 m. Bỏ qua sức cản không khí, bỏ qua các hiệu ứng khác, lấy g = 10 m/s2. Tỉ số giữa số đo đầu và số đo cuối gần giá trị nào nhất sau đây?
Cho hai chất điểm dao động điều hòa cùng phương, cùng tần số, có phương trình dao động lần lượt là = cos(ωt + ), = cos(ωt + ). Cho biết . Khi chất điểm thứ nhất có li độ = 2 cm thì vận tốc của nó có bằng 6 cm/s. Khi đó tốc độ của chất điểm thứ hai là
Một hạt bụi nằm cân bằng trong khoảng giữa hai tấm kim loại song song nằm ngang và nhiễm điện trái dấu. Biết rằng hạt bụi cách bản dưới đoạn d = 0,8cm và hiệu điện thế giữa hai bản tấm kim loại nhiễm điện trái dấu đó là U = 300V. Trong bao lâu hạt bụi sẽ rơi xuống bản dưới, nếu hiệu điện thế giữa hai bản giảm đi một lượng ∆U = 60V? Lấy g = 9,8 .
Đo cường độ dòng điện bằng đơn vị nào sau đây?
Dòng điện chạy trong mạch điện nào dưới đây không phải là dòng điện không đổi?
Trong thời gian t, điện lượng chuyển qua tiết diện thẳng của dây dẫn là q. Cường độ dòng điện không đổi được tính bằng công thức nào?
Các lực lạ bên trong nguồn điện không có tác dụng
Một bộ acquy có thể cung cấp một dòng điện 4 A liên tục trong 1 giờ thì phải nạp lại. Tính cường độ dòng điện mà acquy này có thể cung cấp nếu nó được sử dụng liên tục trong 20 giờ thì phải nạp lại.
Cường độ dòng điện chạy qua dây tóc bóng đèn là I = 0,5 A. Tính điện lượng dịch chuyển qua tiết diện thẳng của dây tóc trong 10 phút.
Cường độ dòng điện chạy qua dây tóc bóng đèn là I = 0,5 A. Tính số electron dịch chuyển qua tiết diện thẳng của dây tóc trong 10 phút?
Một bộ acquy có suất điện động 6 V, sinh ra một công là 360 J khi acquy này phát điện. Thời gian dịch chuyển lượng điện tích này là 5 phút. Tính cường độ dòng điện chạy qua acquy khi đó.
Trong mỗi giây có hạt electron đi qua tiết diện thẳng của một ống phóng điện. Biết điện tích mỗi'hạt có độ lớn bằng 1,6. C. Tính cường độ dòng điện qua ống.
Tính điện lượng dịch chuyển qua tiết diện thẳng của dây tóc trong khoảng thời gian 2 giờ. Biết cường độ dòng điện không đổi chạy qua dây tóc của một bóng đèn là 2,4 A.
Một bộ acquy có suất điện động 12V nối vào một mạch kín. Thời gian dịch chuyến lượng điện tích này là 5 phút. Tính cường độ dòng điện chạy qua acquy này để acquy sản ra công 720 J.
Công suất điện được đo bằng đơn vị nào sau đây?
Điện năng biến đổi hoàn toàn thành nhiệt năng ở dụng cụ hay thiết bị điện nào dưới đây khi chúng hoạt động?
Công suất của nguồn điện được xác định bằng gì?
Khi một động cơ điện đang hoạt động bình thường thì điện năng được biến đổi thành
Đặt hiệu điện thế U vào hai đầu một điện trở R thì dòng điện chạy có cường độ I. Công suất tỏa nhiệt ở điện trở này không thể tính theo bằng công thức nào?
Nhiệt lượng tỏa ra trên dây dẫn khi có dòng điện chạy qua
Một acquy thực hiện công là 12 J khi di chuyển lượng điện tích 2 C trong toàn mạch. Từ đó có thể kết luận là
Một acquy có suất điện động là 12V. Tính công mà acquy này thực hiện khi dịch chuyển một electron bên trong acquy từ cực dương tới cực âm của nó
Một acquy có suất điện động là 12 V. Công suất của acquy này là bao nhiêu nếu có 3,4. electron dịch chuyển bên trong acquy từ cực dương đến cực âm của nó trong một giây?
Tính điện năng tiêu thụ và công suất điện khi dòng điện có cường độ 1 A chạy qua dây dẫn trong 1 giờ. Biết hiệu điện thế giữa hai đầu dây dẫn này là 6 V.
Một nguồn điện có suất điện động 12 V. Khi mắc nguồn điện này với một bóng đèn để tạo thành mạch điện kín thì dòng chạy qua có cường độ 0,8 A. Công của nguồn điện sản ra trong thời gian 15 phút và công suất của nguồn điện lần lượt là
Một bàn là điện khi được sử dụng với hiệu điện thế 220V thì dòng điện chạy qua bàn là có cường độ là 5A. Điện năng bàn là tiêu thụ trong 0,5 h là
Một bàn là điện khi được sử dụng với hiệu điện thế 220 V thì dòng điện chạy qua bàn là có cường độ là 5 A. Tính tiền điện phải trả cho việc sử dụng bàn là này trong 30 ngày, mỗi ngày 20 phút, cho rằng giá tiền điện là 1500 đ /(kWh).
Một đèn ống loại 40 W được chế tạo để có công suất chiếu sáng bằng đèn dây tóc loại 100 W. Hỏi nếu sử dụng đèn ống này trung bình mỗi ngày 5 giờ thì trong 30 ngày sẽ giảm được bao nhiêu tiền điện so với sử dụng đèn dây tóc nói trên? Cho rằng giá tiền điện là 1500 đ/(kWh).
Trên nhãn của một ấm điện có ghi 220 V − 1000 W. Sử dụng ấm điện với hiệu điện thế 220 V để đun sôi 3 lít nước từ nhiệt độ 25°C. Tính thời gian đun nước, biết hiệu suất của ấm là 90% và nhiệt dung riêng của nước là 4190 J/(kgK).
Một ấm điện được dùng với hiệu điện thế 220 V thì đun sôi được 1,5 lít nước từ nhiệt độ 20° c trong 10 phút. Biết nhiệt dung riêng của nước là 4190 J/(kg.K), khối lượng riêng của nước là 1000 kg/ và hiệu suất của ấm là 90 %. Công suất vả điện trở của ấm điện lần lượt là
Trên một bóng đèn dây tóc có ghi 12 V − 1,25 A. Kết luận nào dưới đây là sai?
Bóng đèn sợi đốt 1 có ghi 220 V − 100 W và bóng đèn sợi đốt 2 có ghi 220 V − 25 W. Mắc nối tiếp hai đèn này vào hiệu điện thế 220 V thì công suất tiêu thụ của các đèn lần lượt là . Cho rằng điện trở của mỗi đèn có giá trị không đổi. Chọn phương án đúng.
Cho mạch điện gồm hai điện trở mắc nối tiếp nhau và mắc vào nguồn điện có hiệu điện thế U = 9V. Cho = 1,5 Ω. Biết hiệu điện thế hai đầu là 6V. Tính nhiệt lượng tỏa ra trên trong 2 phút.
Một quạt điện được sử dụng dưới hiệu điện thế 220 V thì dòng điện chạy qua quạt có cường độ là 5 A. Tính nhiệt lượng mà quạt tỏa ra trong 30 phút theo đơn vị Jun.
Một bộ acquy có suất điện động 6V có dung lượng là 15Ah. Acquy này có thể sử dụng thời gian bao lâu cho tới khi phải nạp lại. Tính điện năng tương ứng dự trữ trong acquy nếu coi nó cung cấp dòng điện không đổi 0,5A.
Một acquy có suất điện động = 2 V, có dung lượng q = 240 A.h. Tính điện năng của acquy.
Số đếm của công tơ điện gia đình cho biết điều gì?
Điện trở tiêu thụ một công suất P khi được mắc vào một hiệu điện thế U không đổi. Nếu mắc song song với một điện trở rồi mắc vào hiệu điện thế U nói trên thì công suất tiêu thụ bởi sẽ
Điện trở tiêu thụ một công suất P khi được mắc vào một hiệu điện thế U không đổi. Nếu mắc nối tiếp với một điện trở rồi mắc vào hiệu điện thế U nói trên thì công suất tiêu thụ bởi sẽ
Điện năng biến đổi hoàn toàn thành nhiệt năng ở dụng cụ hay thiết bị nào dưới đây khi chúng hoạt động?
Công suất định mức của các dụng cụ điện là
Có hai điện trở mắc giữa hai điểm có hiệu điện thế 12 V. Khi nối tiếp thì công suất của mạch là 4 W. Khi R1 mắc song song thì công suất mạch là 18 W. Hãy xác định và .
Ba điện trở giống nhau được mắc như hình, nếu công suất tiêu thụ trên điện trở (1) là 3 W thì công suất toàn mạch là bao nhiêu?
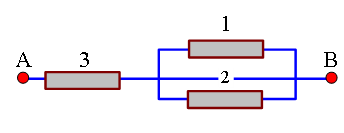
Ba điện trở bằng nhau = = mắc như hình vẽ. Công suất tiêu thụ
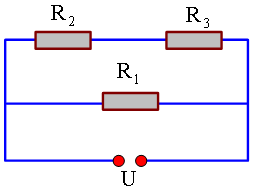
Một điện trở R = 4Ω được mắc vào nguồn điện có suất điện động 1,5V để tạo thành mạch kín thì công suất tỏa nhiệt ở điện trở này là 0,36W. Hiệu điện thế giữa hai đầu điện trở R và điện trở trong của nguồn điện lần lượt là
Mắc một điện trở 14 Ω vào hai cực của một nguồn điện có điện trở trong là 1 Ω thì hiệu điện thế giữa hai cực của nguồn là 8,4 V. Công suất mạch ngoài và công suất của nguồn điện lần lượt là
Một nguồn điện có suất điện động 6V, điện trở trong 2 Ω mắc với mạch ngoài là một biến trở R để tạo thành một mạch kín. Tính R để công suất tiêu thụ của mạch ngoài là 4W.
Một nguồn điện có suất điện động 12 V và điện trở trong 2 Ω. Nối điện trở R vào hai cực của nguồn điện thành mạch kín thì công suất tiêu thụ trên điện trở R bằng 16 W. Biết giá trị của điện trở R < 2 Ω. Hiệu suất của nguồn là
Nguồn điện có suất điện động là 3V và có điện trở trong là 1 Ω. Mắc song song hai bóng đèn như nhau có cùng điện trở 6 Ω vào hai cực của nguồn điện này. Công suất tiêu thụ điện của mỗi bóng đèn là
Cho mạch điện như hình vẽ. Trong đó, = 11Ω, R = 0,9 Ω. Biết đèn dây tóc sáng bình thường. Hiệu điện thế định mức và công suất định mức của bóng đèn lần lượt là
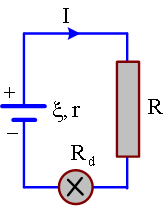
Ba điện trở có trị số R, 2R, 3R mắc như hình vẽ. Nếu công suất của điện trở (1) là 8 W thì công suất của điện trở (3) là bao nhiêu?

Một nguồn điện có suất điện động = 12V điện trở trong r = 2Ω nối với điện trở R tạo thành mạch kín. Tính cường độ dòng điện và hiệu suất nguồn điện, biết R > 2Ω, công suất mạch ngoài là 16W.
Cho mạch điện như hình vẽ. Trong đó = 6 V, r = 0,5Ω, = 1 Ω, = = 4 Ω, = 6 Ω. Chọn phương án đúng.
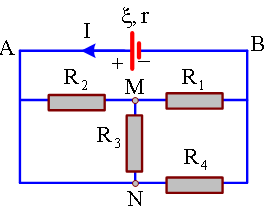
Một acquy có suất điện động = 2V, điện trở trong r = 1 Ω. Nối hai cực acquy với một điện trở R = 9 Ω thì công suất tiêu thụ trên mạch ngoài là bao nhiêu? Tính hiệu suất của acquy.
Mạch kín gồm acquy = 2,2V cung cấp điện năng cho điện trở mạch ngoài R = 0,5Ω. Hiệu suất của acquy H = 65%. Tính cường độ dòng điện trong mạch.
Một dây hợp kim có điện trở là R = 5 Ω được mắc vào hai cực của một pin điện hoá có suất điện động 1,5 V và điện trở trong là 1 Ω. Điện trở của các dây nối là rất nhỏ. Trong thời gian 5 phút, lượng hoá năng được chuyển hoá thành điện năng và nhiệt lượng tỏa ra ở điện trở R lần lượt là
Cho mạch điện có sơ đồ như hình vẽ, trong đó các acquy có suất điện động = 12 V, = 6 V và có điện trở trong không đáng kể. Các điện trở = 4 Ω; = 8 Ω. Chọn phương án đúng.
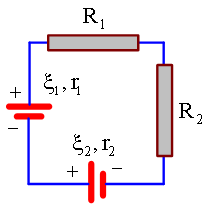
Khi nhiệt độ tăng thì điện trở của chất điện phân
Khối lượng khí clo sản xuất ra cực dương của các bình điện phân 1, 2 và 3 (xem hình vẽ) trong một khoảng thời gian nhất định sẽ
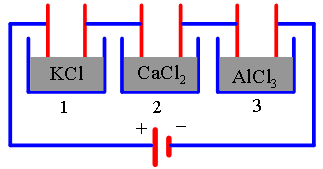
Để tiến hành các phép đo cần thiết cho việc xác định đương lượng điện hóa của một kim loại nào đó, ta cần phải sử dụng các thiết bị
Khi điện phân dung dịch nhôm ôxit nóng chảy, người ta cho dòng điện cường độ 20 kA chạy qua dung dịch này tương ứng với hiệu điện thế giữa các điện cực là 5,0 V. Nhôm có khối lượng mol là A = 27 g/mol và hóa trị n = 3. Để thu được 1 tấn nhôm thời gian điện phân và lượng điện năng đã tiêu thụ lần lượt là
Người ta muốn bóc một lớp đồng dày d = 10 µm trên một bản đồng diện tích S = 1 bằng phương pháp điện phân. Cường độ dòng điện là 0,01 A. Biết đương lượng gam của đồng là 32 g/mol, khối lượng riêng của đồng là 8900 . Tính thời gian cần thiết để bóc được lớp đồng.
Chiều dày của một lớp niken phủ lên một tấm kim loại là h = 0,00496 cm sau khi điện phân trong 30 phút. Diện tích mặt phủ của tấm kim loại là S = 30 . Biết niken có A = 58, n = 2 và có khối lượng riêng là D = 8,9 g/. Cường độ dòng điện chạy qua bình điện phân là
Muốn mạ đồng một tấm sắt có diện tích tổng cộng 200 , người ta dùng tấm sắt làm catôt của một bình điện phân đựng dung dịch và anôt là một thanh đồng nguyên chất, rồi cho dòng điện có cường độ I = 10 A chạy qua trong thời gian 2 giờ 40 phút 50 giây. Cho biết đồng có A = 64; n = 2 và có khối lượng riêng D = 8,9.103 kg/. Tìm bề dày lớp đồng bám trên mặt tấm sắt.
Hai bình điện phân (Fe/Fe và CuS/Cu) mắc nối tiếp. Sau một khoảng thời gian bình thứ nhất giải phóng một lượng sắt là 1,4 gam. Biết khối lượng mol của đồng và sắt là 64 và 56, hóa trị của đồng và sắt là 2 và 3. Tính lượng đồng giải phóng ở bình thứ hai trong cùng khoảng thời gian đó?
Hai bình điện phân CuS/Cu và AgN/Ag mắc nối tiếp trong một mạch điện. Sau một thời gian điện phân, tổng khối lượng catot của hai bình tăng lên 2,8g. Biết khối lượng mol của đồng và bạc là 64 và 108, hóa trị của đồng và bạc là 2 và 1. Gọi điện lượng qua các bình điện phân là q, khối lượng Cu và Ag được giải phóng ở catot lần lượt là và . Chọn phương án đúng.
Hai bình điện phân CuS/Cu và AgN/Ag mắc nối tiếp, trong một mạch điện có cường độ 0,5 A. Sau thời gian điện phân t, tổng khối lượng catôt của hai bình tăng lên 5,6 g. Biết khối lượng mol của đồng và bạc là 64 và 108, hóa trị của đồng và bạc là 2 và 1. Tính t.
Một bình điện phân chứa dung dịch bạc nitrat (AgN) có điện trở 2 Ω. Anôt của bình bằng bạc và hiệu điện thế đặt vào hai điện cực của bình điện phân là 12 V. Biết bạc có A = 108 g/mol, có n = 1. Khối lượng bạc bám vào catôt của bình điện phân sau 16 phút 5 giây là
Một bình điện phân đựng dung dịch CuS, với các cực điện cực đều bằng đồng, diện tích catot bằng 10 , khoảng cách từ catot đến anot là 5 cm. Đương lượng gam của đồng là 32. Hiệu điện thế đặt vào U = 15 V, điện trở suất của dung dịch là 0,2 Ωm. Sau thời gian t = 1 h, khối lượng đồng bám vào catot gần giá trị nào nhất sau đây?
Một bình điện phân chứa dung dịch bạc nitrat (AgN) có điện trở 2Ω. Anot của bình bằng bạc có đương lượng gam là 108. Nối hai cực của bình điện phân với nguồn điện có suất điện động 12V và điện trở trong 2 Ω. Khối lượng bạc bám vào catot của bình điện phân 16 phút 5 giây là
Một bộ nguồn điện gồm 30 pin mắc thành 3 nhóm nối tiếp, mỗi nhóm có 10 pin mắc song song; mỗi pin có suất điện động 0,9 V và điện trở trong 0,6 Ω. Một bình điện phân đựng dung dịch CuS có điện trở 1,82 Ω được mắc vào hai cực của bộ nguồn nói trên. Anôt của bình điện phân bằng đồng. Biết Cu có A = 64; n = 2. Tính khối lượng đồng bám vào catôt của bình trong thời gian 50 phút.
Người ta dùng 36 nguồn giống nhau, mỗi nguồn có suất điện động 1,5 V, điện trở trong 0,9 Ω để cung cấp điện cho một bình điện phân đựng dung dịch ZnS với cực dương bằng kẽm, có điện trở R = 3,6 Ω. Biết đương lượng gam của kẽm là 32,5. Bộ nguồn được mắc thành n dãy song song trên mỗi dãy có m nguồn nối tiếp thì khối lượng kẽm bám vào catôt trong thời gian 1 giờ 4 phút 20 giây là lớn nhất và bằng
Cho mạch điện như hình vẽ. Biết nguồn có suất điện động 24 V, điện trở trong 1Ω tụ điện có điện dung C = 4 µF; đèn Đ loại 6 V - 6 W; các điện trở có giá trị = 6 Ω; = 4 Ω bình điện phân đựng dung dịch CuS và có anốt làm bằng Cu, có điện trở = 2 Ω. Đương lượng gam của đồng là 32. Coi điện trở của đèn không đổi. Khối lượng Cu bám vào catôt sau 16 phút 5 giây và điện tích của tụ điện lần lượt là
Cho mạch điện như hình vẽ. Trong đó bộ nguồn có n pin mắc nối tiếp, mỗi pin có suất điện động 1,5V và điện trở trong 0,5Ω. Mạch ngoài gồm các điện trở = 20Ω, = 9 Ω, = 2 Ω, đèn Đ loại 3V – 3W, là bình điện phân đựng dung dịch AgN, có cực dương bằng bạc. Điện trở của ampe kế và dây nối không đáng kể, điện trở của vôn kế rất lớn. Biết ampe kế chỉ 0,6A, ampe kế chỉ 0,4A. Coi điện trở của đèn không đổi. Đương lượng gam của bạc là 108. Chọn phương án đúng.
Cho mạch điện như hình vẽ. Ba nguồn điện giống nhau = 3 Ω, = 6 Ω, bình điện phân chứa dung dịch CuS với cực dương bằng đồng và có điện trở = 0,5 Ω. Đương lượng gam của đồng là 32. Sau một thời gian điện phân 386 giây người ta thấy khối lượng của bản cực làm catot tăng lên 0,64g. Dùng một vôn có điện trở rất lớn mắc vào 2 đầu A và C của bộ nguồn. Nếu bỏ mạch ngoài đi thì vôn kế chỉ 20V. Điện trở của mỗi nguồn điện là
Cho mạch điện như hình vẽ. Bộ nguồn gồm 6 nguồn giống nhau, mỗi nguồn có suất điện động 2,25V, điện trở trong 0,5Ω. Bình điện phân có điện trở chứa dung dịch CuS, anot làm bằng đồng. Đương lượng gam của đồng là 32. Tụ điện có điện dung C = 6 . Đèn Đ loại 4V – 2W, các điện trở có giá trị = 0,5 = = 1Ω. Biết đèn Đ sáng bình thường. Chọn phương án đúng.
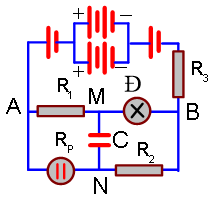
Cho mạch điện như hình vẽ. Trong đó bộ nguồn gồm 8 nguồn giống nhau mỗi cái có suất điện động 5V, có điện trở trong 0,25Ω mắc nối tiếp, đèn Đ có 4 loại 4V – 8W, = 3Ω, = = 2 Ω, = 4 Ω và RP là bình điện phân đựng dung dịch có cực dương bằng Al. Đương lượng gam của nhôm là 9. Điều chỉnh biến trở để đèn Đ sáng bình thường thì
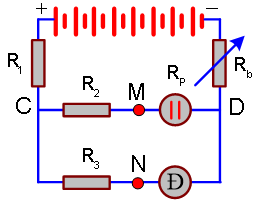
Cho mạch điện như hình vẽ. Trong đó bộ nguồn gồm 8 nguồn giống nhau mỗi cái có suất điện động 1,5V, có điện trở trong 0,5Ω mắc thành 2 nhánh, mỗi nhánh có 4 nguồn mắc nối tiếp. Đèn Đ loại 3V – 3W, = 2Ω, = 3 Ω, = 2 Ω, Rp = 1 Ω và là bình điện phân đựng dung dịch CuS có cực dương bằng Cu. Biết Cu có khối lượng mol 64 và có hóa trị 2. Coi điện trở của đèn không thay đổi. Khối lượng Cu giải phóng ra ở cực âm trong thời gian 32 phút 10 giây và hiệu điện thế lần lượt là
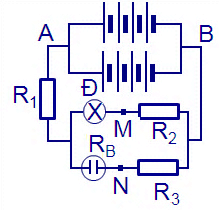
Hai thanh ray dẫn điện dài song song với nhau, khoảng cách giữa hai thanh ray là 0,4 m. Hai thanh dẫn điện MN và PQ có cùng điện trở 0,25 Ω, được gác tiếp xúc điện lên hai thanh ray và vuông góc với hai ray. Điện trở R = 0,5 Ω, tụ điện C = 20 pF ban đầu chưa tích điện, bỏ qua điện trở của hai ray và điện trở tiếp xúc. Tất cả hệ thống được đặt trong một từ trường đều có vectơ cảm ứng từ vuông góc với mặt phẳng hình vẽ chiều đi vào trong, độ lớn B = 0,2 T. Cho thanh MN và PQ trượt hai hướng ngược nhau với tốc độ lần lượt 0,5 m/s và 1 m/s. Công suất tỏa nhiệt trên điện trở R gần giá trị nào nhất sau đây?
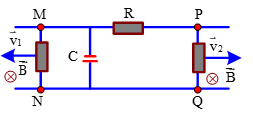
Hai dây siêu dẫn thẳng dài, song song, cách nhau một khoảng ℓ, đặt trên mặt phẳng ngang, ở giữa mỗi dây nối với điện trở R. Hai thanh kim loại nhẵn AB và CD có cùng điện trở R, chỉ có thể trượt không ma sát trên hai thanh siêu dẫn nói ừên. Tác dụng lên AB, CD các lực song song với hai thanh siêu dẫn để chúng chuyển động thẳng đều về hai phía với các tốc độ lần lượt là và như hình vẽ. Nếu thanh AB chuyển động trong từ trường đều thẳng đứng hướng lên với độ lớn ; còn CD chuyển động trong từ trường đều thẳng đứng hướng trên xuống với độ lớn thì
Một cái đĩa phẳng không dẫn điện, bán kính R, người ta kẹp vào theo đường dây cung một thanh siêu dẫn MN = 16 cm với I là trung điểm. Đĩa được quay đều với tốc độ góc ω = 100 rad/s, quanh trục đi qua tâm đĩa vuông góc với mặt phẳng đĩa, trong từ trường đều có độ lớn B = 0,5 T, có phương song song với trục quay. Hiệu điện thế là

Một người đi thang máy từ tầng G xuống tầng hầm B2, rồi lên tới tầng 15 của toà nhà. Biết mỗi tầng cách nhau 3 m. Tính độ dịch chuyển và quãng đường đi được của người đó:
a) Khi đi từ tầng G xuống tầng hầm B2.
b) Khi đi từ tầng hầm B2 lên tầng 15.
c) Trong cả chuyến đi.
Thị trấn A cách thị trấn B là 20,0 km theo đường thẳng. Một người đi xe đạp rời thị trấn A và đi đến thị trấn B với tốc độ 20,0 km/h. Vào đúng thời điểm đó, người đi xe đạp thứ hai rời thị trấn B đi đến thị trấn A với tốc độ 15,0 km/h.
a) Hai người đi xe đạp sẽ gặp nhau ở đâu giữa hai thị trấn?
b) Tìm khoảng thời gian từ lúc xuất phát đến khi họ gặp nhau.
Một người đi bộ 5,0 km trên một con đường thẳng theo hướng bắc rồi quay đầu lại và đi 12 km theo hướng nam. Tìm:
a) Tổng quãng đường đã đi.
b) Độ dịch chuyển.
Một chiếc thuyền đi xuôi dòng 1,6 km rồi quay đầu đi ngược dòng 1,2 km. Toàn bộ chuyến đi mất 45 phút. Tìm:
a) Tốc độ trung bình của thuyền.
b) Độ dịch chuyển của thuyền.
c) Vận tốc trung bình của thuyền.
Một người đi bộ với tốc độ không đổi 5,00 m/s dọc theo đường thẳng từ A đến B rồi đi ngược lại theo đường thẳng đó từ B đến A với tốc độ không đổi 3,00 m/s.
a) Tốc độ trung bình của người ấy trong toàn bộ chuyến đi là bao nhiêu?
b) Tìm vận tốc trung bình của người ấy trong toàn bộ chuyến đi.
Một xe thí nghiệm chuyển động trên đường thẳng. Độ dịch chuyển của nó theo thời gian được thể hiện trong bảng 1.
| t (s) | 0 | 1,0 | 2,0 | 3,0 | 4,0 | 5,0 |
| d (m) | 0 | 2,3 | 9,2 | 20,7 | 36,8 | 57,5 |
Tìm vận tốc trung bình của xe:
a) Trong 1 giây đầu tiên.
b) Trong 3 giây cuối.
c) Trong toàn bộ thời gian quan sát.
Bạn Lan chơi trò chơi tìm kho báu ở ngoài vườn với các bạn của mình. Bạn Lan giấu kho báu của mình là một chiếc nơ vào trong một cái hộp rồi viết mật thư tìm kho báu như sau: Bắt đầu từ gốc cây mận, đi 10 bước về phía Bắc, sau đó đi 7 bước về phía Đông, 12 bước về phía Nam, 9 bước về phía Tây là tới chỗ giấu kho báu.
a) Hãy tính quãng đường phải đi (theo bước) để tìm ra kho báu.
b) Tính độ dịch chuyển (theo bước) để tìm ra kho báu.
Cho đồ thị độ dịch chuyển - thời gian của hai xe chuyển động trên cùng đường thẳng.
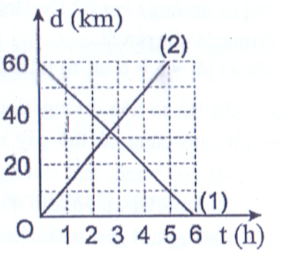
a) Nhận xét về tính chất chuyển động, tính vận tốc của mỗi xe.
b) Lập phương trình độ dịch chuyển – thời gian của hai xe.
c) Xác định thời điểm và vị trí hai xe gặp nhau.
Số liệu về độ dịch chuyển và thời gian của chuyển động thẳng của một xe ô tô đồ chơi chạy bằng pin được ghi trong bảng sau.
|
Độ dịch chuyển (m) |
1 |
3 |
5 |
7 |
7 |
7 |
|
Thời gian (s) |
0 |
1 |
2 |
3 |
4 |
5 |
a) Vẽ đồ thị dịch chuyển - thời gian chuyển động.
b) Mô tả chuyển động của xe.
c) Tính vận tốc của xe trong 3 s đầu.
Nhà của Đăng và trường nằm trên cùng một con đường nên hằng ngày Đăng đều đi học bằng xe đạp từ nhà đến trường với tốc độ không đổi bằng 4 m/s (khi trời lặng gió). Trong một lần Đăng đạp xe từ nhà đến trường, có một cơn gió thổi ngược chiều trong khoảng thời gian 90 s. Hình vẽ mô tả đồ thị độ dịch chuyển - thời gian của Đăng trong 5 phút đầu tiên. Tìm tốc độ của gió so với mặt đất.
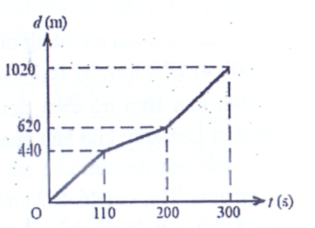
Cho đồ thị độ dịch chuyển - thời gian của ô tô chuyển động thẳng theo một hướng xác định. Ô tô đi với tốc độ lớn nhất trong đoạn đường nào? Vì sao?
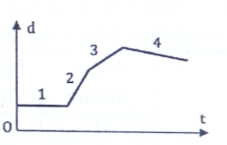
Đồ thị độ dịch chuyển - thời gian trong chuyển động thẳng của một xe ô tô đồ chơi điều khiển từ xa được vẽ ở hình bên.
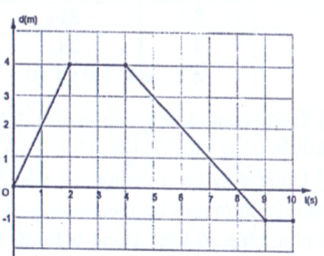
a) Mô tả chuyển động của xe.
b) Xác định vị trí của xe so với điểm xuất phát của xe ở giây thứ 2, giây thứ 4, giây thứ 8 và giây thứ 10.
c) Xác định tốc độ và vận tốc của xe trong 2 giây đầu, từ giây 2 đến giây 4 và từ giây 4 đến giây 8.
d) Xác định quãng đường đi được và độ dịch chuyển của xe sau 10 giây chuyển động. Tại sao giá trị của chúng không giống nhau?
Cho đồ thị độ dịch chuyển - thời gian của An đang bơi trong bể bơi dài 50 m. Đồ thị này cho biết những gì về chuyển động của An?
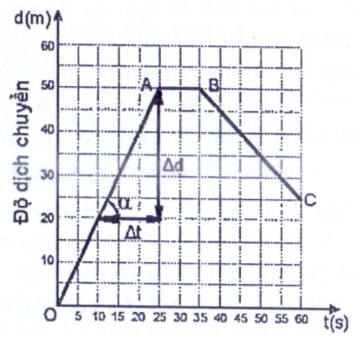
a) Mô tả chuyển động của An.
b) Xác định quãng đường và tốc độ của An trong các đoạn OA, AB và BC.
c) Xác định độ dịch chuyển và vận tốc của người đó trong cả quá trình bơi.
Một người đi bộ 3,0 km theo hướng Nam rồi 2,0 km theo hướng Tây.
a) Vẽ giản đồ vectơ để minh họa các độ dịch chuyển.
b) Tìm độ dịch chuyển tổng hợp.
Đồ thị độ dịch chuyển - thời gian của một chuyển động thẳng được cho như hình vẽ.

A) Hãy mô tả chuyển động.
B) Xác định tốc độ và vận tốc của chuyển động trong các khoảng thời gian:
a) Từ 0 đến 0,5 h. b) Từ 0,5 đến 2,5 h.
c) Từ 0 đến 3,25 h. d) Từ 0 đến 5,5 h.
An và Bình đi xe đạp theo một con đường thẳng. Tại thời điểm t = 0, An đang đi với tốc độ không đổi là 3,0 m/s qua chỗ Bình đang ngồi trên xe đạp đứng yên. Cũng tại thời điểm đó, Bình bắt đầu đuổi theo An. Tốc độ của Bình tăng đều từ thời điểm t = 0 s đến t = 5 s, khi đi được 10 m. Sau đó Bình tiếp tục đi với tốc độ không đổi là 4,0 m/s.
a) Vẽ đồ thị độ dịch chuyển - thời gian của An, từ t = 0 s đến t = 12 s.
b) Khi nào Bình đuổi kịp An?
c) Từ lúc chuyển động với tốc độ không đổi, Bình đi thêm bao nhiêu mét nữa thì gặp được An?
Bạn An và bạn Bình ở hai đầu một đoạn đường thẳng AB dài 10 km đi bộ đến gặp nhau. Bạn An đi trước bạn Bình 0,5 h. Sau khi bạn Bình đi được 1 h thì hai bạn gặp nhau. Biết hai bạn đi cùng tốc độ.
a) Tính vận tốc của hai bạn.
b) Viết phương trình chuyển động của hai bạn.
c) Vẽ đồ thị độ dịch chuyển - thời gian cho chuyển động của hai bạn trên cùng một hệ trục toạ độ.
d) Xác định vị trí và thời điểm hai người gặp nhau.
Một người điều khiển thuyền đi được 5,6 km theo hướng Bắc trên mặt hồ phẳng lặng trong thời gian 1,0 h. Sau đó, anh ta quay thuyền đi về phía Tây 3,4 km trong 30,0 phút.
a) Tìm độ dịch chuyển tổng hợp của thuyền.
b) Xác định vận tốc trung bình của chuyến đi.
Một người đang ở phía tây của một cái hồ và muốn bơi ngang qua để đến vị trí ở phía đông, đối diện với vị trí xuất phát của mình. Người này có thể bơi với vận tốc 1,9 m/s khi nước hồ lặng. Biết rằng lá cây trôi trên mặt nước hồ được 4,2 m về hướng nam trong 5,0 s.
a) Người này sẽ phải bơi theo hướng nào để đến vị trí đối diện trực tiếp với vị trí của anh ta?
b) Tìm vận tốc tổng hợp của người đó.
c) Nếu hồ rộng 4,8 km thì người đó phải bơi bao nhiêu phút?
Một canô chạy qua sông xuất phát từ A, mũi hướng tới điểm B bờ bên kia. AB vuông góc với bờ sông. Nhưng do nước chảy, nên khi đến bên kia, canô lại ở C cách B đoạn BC = 200 m. Thời gian qua sông là 1 phút 40 giây.
Nếu người lái giữ cho mũi canô chếch so với bờ sông và mở máy chạy như trước thì canô tới đúng vị trí B. Hãy tính:
a) Vận tốc nước chảy và vận tốc canô.
b) Bề rộng của dòng sông.
c) Thời gian qua sông của canô lần sau.
Ở một đoạn sông thẳng, dòng nước có vận tốc , một thuyền chuyển động đều có vận tốc so với nước luôn có độ lớn là từ A.
- Nếu người lái hướng mũi thuyền theo B thì sau 10 phút, thuyền tới C phía hạ lưu với BC = 120 m.
- Nếu người lái hướng mũi thuyền về phía thượng lưu theo góc lệch α thì sau 12 phút 30 giây thuyền tới đúng B.
a) Tính vận tốc thuyền và bề rộng L của sông.
b) Xác định góc lệch α.
Một canô muốn đi thẳng qua một con sông rộng 0,10 km. Động cơ của canô tạo cho nó vận tốc 4,0 km/h trong nước sông không chảy. Tuy nhiên, có một dòng chảy mạnh đang di chuyển về phía hạ lưu với vận tốc 3,0 km/h.
a) Canô phải đi theo hướng nào để đến vị trí ở bờ bên kia đối diện với vị trí xuất phát?
b) Chuyến đi sẽ mất bao nhiêu phút?
Một ô tô đang đi với tốc độ 14 m/s thì gặp đèn đỏ phía trước. Người lái hãm phanh và ô tô dừng lại sau 5,0 s. Tính gia tốc của ô tô.
Một chiếc xe thể thao đang chạy với tốc độ 110 km/h thì hãm phanh và dừng lại trong 6,1 giây. Tìm gia tốc của nó.
Một ô tô đang đi với vận tốc 50,0 km/h theo hướng bắc thì quay đầu đi về hướng tây với vận tốc 50,0 km/h. Tổng thời gian đi là 5,0 s. Tìm:
a) độ thay đổi vận tốc.
b) gia tốc của xe.
Một ô tô thể thao tăng tốc trên đường thẳng từ trạng thái đứng yên lên 70 km/h trong 6,3 s. Gia tốc trung bình của nó là bao nhiêu?
Một đoàn tàu đang đi trên đường thẳng với tốc độ 115 km/h. Tàu phanh và mất 1,5 phút để dừng lại. Tính gia tốc trung bình của nó.
Một vận động viên chạy nước rút, đạt tốc độ tối đa là 9,0 m/s trong 1,5 giây. Tính gia tốc trung bình của vận động viên này.
Đồ thị vận tốc - thời gian của một vật chuyển động dọc theo trục Ox được thể hiện trong hình vẽ. Xác định gia tốc trung bình của vật trong các khoảng thời gian:
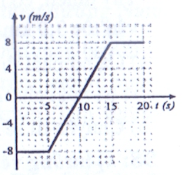
a) t = 5,00 s đến t = 15,0 s.
b) t = 0 đến t = 20,0 s.
Trên hình vẽ a), b) và c) là đồ thị vận tốc - thời gian (v - t) của các vật chuyển động thẳng theo một hướng xác định. Các đồ thị gia tốc theo thời gian của các chuyển động này (a - t), được biểu diễn theo thứ tự xáo trộn là d), e) và g). Hãy chọn từng cặp đồ thị v - t và đồ thị a – t ứng với mỗi chuyển động. Giải thích.
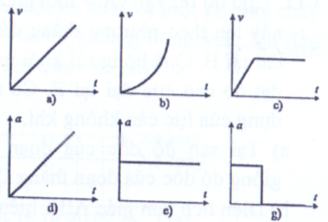
Xét một người đi xe máy trên một đoạn đường thẳng. Tốc độ của xe máy tại mỗi thời điểm được ghi lại trong bảng dưới đây.
|
t (s) |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
|
v (m/s) |
0 |
15 |
30 |
30 |
20 |
10 |
0 |
a) Vẽ đồ thị vận tốc - thời gian của xe máy.
b) Nhận xét tính chất chuyển động của xe máy.
c) Xác định gia tốc của xe máy trong 10 s đầu tiên và trong 15 s cuối cùng.
d) Từ đồ thị vận tốc - thời gian, tính quãng đường và tốc độ trung bình mà người này đã đi được sau 30 s kể từ lúc bắt đầu chuyển động.
Cho đồ thị vận tốc - thời gian của một quả bóng thả rơi chạm đất rồi nảy lên theo phương thẳng đứng. Quả bóng được thả tại A và chạm đất tại B. Quả bóng rời khỏi mặt đất tại D và đạt độ cao cực đại tại E. Có thể bỏ qua tác dụng của lực cản không khí.
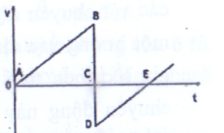
a) Tại sao độ dốc của đoạn thẳng AB lại giống độ dốc của đoạn thẳng DE?
b) Diện tích tam giác ABC biểu thị đại lượng nào?
c) Tại sao diện tích tam giác ABC lớn hơn diện tích tam giác CDE?
Một quả bóng bàn được bắn ra theo phương ngang với vận tốc đầu bằng không đến va chạm vào tường và bật lại trong khoảng thời gian rất ngắn. Hình vẽ là đồ thị vận tốc - thời gian mô tả chuyển động của quả bóng trong 20 s đầu tiên. Tính quãng đường mà quả bóng bay được sau 20 s kể từ lúc bắt đầu chuyển động.
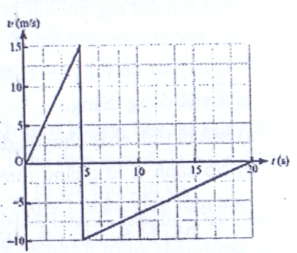
Quan sát đồ thị vận tốc - thời gian mô tả chuyển động thẳng của tàu hỏa và trả lời các câu hỏi sau:
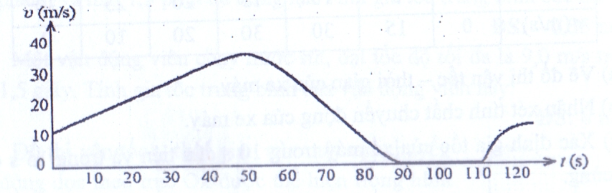
a) Tại thời điểm nào, vận tốc tàu hỏa có giá trị lớn nhất?
b) Vận tốc tàu hỏa không đổi trong khoảng thời gian nào?
c) Tàu chuyển động thẳng nhanh dần đều trong khoảng thời gian nào?
Cho đồ thị vận tốc - thời gian của một xe buýt và một xe máy chạy trên một đường thẳng. Xe buýt đang đứng yên, bắt đầu chuyển động thì xe máy đi tới vượt lên trước xe buýt.
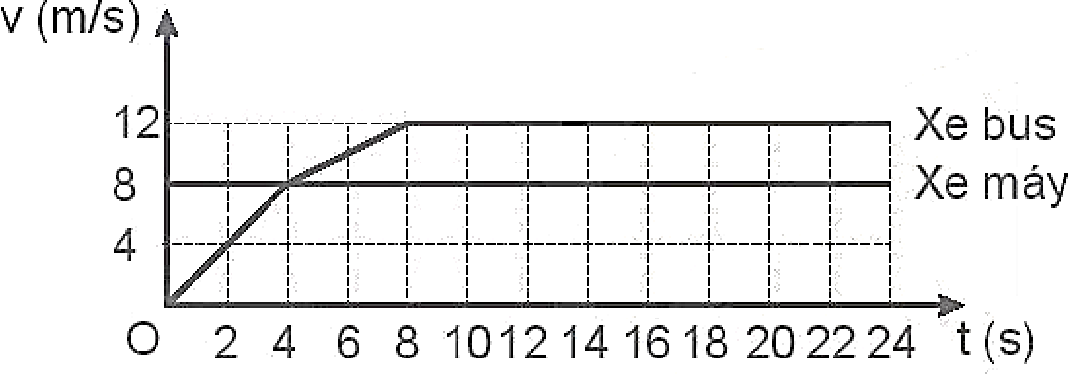
a) Tính gia tốc của xe buýt trong 4 s đầu và trong 4 s tiếp theo.
b) Khi nào thì xe buýt bắt đầu chạy nhanh hơn xe máy?
c) Khi nào thì xe buýt đuổi kịp xe máy?
d) Xe máy đi được bao nhiêu mét thì bị xe buýt đuổi kịp?
e) Tính vận tốc trung bình của xe buýt trong 8 s đầu.
Hai xe ô tô 1 và 2 chuyển động thẳng cùng chiều. Xe 1 đang đi với tốc độ không đổi 72 km/h thì vượt xe 2 tại thời điểm t = 0. Để đuổi kịp xe 1, xe 2 đang đi với tốc độ 45 km/h ngay lập tức tăng tốc đều trong 10 s để đạt tốc độ không đổi 90 km/h. Tính:
a) Quãng đường xe 1 đi được trong 10 s đầu tiên, kể từ lúc t = 0.
b) Gia tốc và quãng đường đi được của xe 2 trong 10 s đầu tiên.
c) Thời gian cần thiết để xe 2 đuổi kịp xe 1.
d) Từ t = 0 đến khi hai xe gặp nhau, tính quãng đường mỗi xe đi được.
Một vật chuyển động với đồ thị vận tốc - thời gian như hình vẽ.
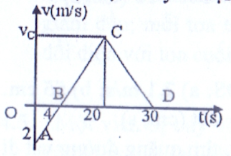
a) Tính gia tốc và nêu tính chất chuyển động cho từng giai đoạn.
b) Viết phương trình vận tốc cho từng giai đoạn với cùng một gốc thời gian chọn lúc ban đầu.
c) Tính quãng đường vật đã đi được và vận tốc trung bình của vật.
Một xe ô tô đang chuyển động với vận tốc 36 km/h thì xuống dốc dài 400 m theo một chuyển động thẳng nhanh dần đều; trong thời gian 20 s thì ô tô xuống hết dốc.
a) Tìm thời gian xe đi hết 58 m cuối dốc.
b) Khi xuống hết đốc xe hãm thắng chuyển động chậm dần đều thêm 50 m nữa thì dừng hẳn. Tìm thời gian xe đi hết quãng đường này.
c) Vẽ đồ thị vận tốc - thời gian mô tả các quá trình chuyển động của xe.
Một ô tô bắt đầu khởi hành từ A chuyển động thẳng nhanh dần đều về B với gia tốc 0,5 m/. Cùng lúc ô tô bắt đầu qua A, một xe máy đi qua B cách A 125 m với vận tốc 18 km/h, chuyển động thẳng nhanh dần đều về phía A với gia tốc 30 cm/. Tìm:
a) Vị trí hai xe gặp nhau và vận tốc của mỗi xe lúc đó.
b) Quãng đường mà mỗi xe đi được kể từ lúc ô tô khởi hành từ A.
Phương trình chuyển động của vật: x = 80 + 50t + 10 (cm; s)
a) Tính vận tốc lúc t = 1 s.
b) Định vị trí vật lúc vận tốc là 130 cm/s.
Một người đi xe đạp đang đi với vận tốc 5,6 m/s thì bắt đầu gia tốc 0,60 m/ trong khoảng thời gian 4,0 s.
a) Tìm quãng đường người ấy đã đi cả khoảng thời gian này.
b) Tìm vận tốc cuối cùng sau khi tăng tốc.
Một xe ô tô đang đi với tốc độ 22 m/s thì người lái xe nhận thấy biển báo hạn chế tốc độ ở phía trước. Anh ta giảm dần đều tốc độ của xe đến 14 m/s. Trong quá trình giảm tốc độ, người đó đi được quãng đường 125 m.
a) Tìm gia tốc của xe.
b) Người lái xe đã mất bao lâu để thay đổi vận tốc?
Một ô tô đang đi trên đường thẳng với tốc độ không đổi 24 m/s. Ô tô này đã chạy quá tốc độ và vượt qua một cảnh sát giao thông đang ngồi trên một xe mô tô đứng yên. Người cảnh sát ngay lập tức đuổi theo ô tô với gia tốc 2,1 m/. Từ thời điểm ô tô vượt qua xe cảnh sát:
a) sau bao lâu thì xe cảnh sát đuổi kịp ô tô?
b) các xe sẽ đi được quãng đường bao nhiêu mét trong thời gian đó?
Một học sinh đang đứng ở chỗ đợi tàu trên sân của một nhà ga, nhận thấy rằng hai toa đầu tiên của một đoàn tàu đến vượt qua mình trong 2,0 giây và hai toa tiếp theo trong 2,4 giây. Tốc độ của đoàn tàu đang giảm đều; mỗi toa tàu dài 20 m. Khi tàu dừng thì học sinh đó đứng đối điện với toa cuối cùng. Đoàn tàu có bao nhiêu toa?
Một viên bi bay với tốc độ 25,0 m/s vuông góc với một bức tường và bật ngược lại với tốc độ 22,0 m/s. Nếu viên bi tiếp xúc với tường trong thời gian 3,50 m/s thì gia tốc trung bình của nó trong khoảng thời gian này là bao nhiêu? Biết 1 ms = s.
Một ô tô chuyển động chậm dần đều, trong 8,50 s đi được quãng đường 40,0 m với vận tốc cuối cùng là 2,80 m/s.
a) Tìm độ lớn vận tốc ban đầu của xe.
b) Tìm gia tốc của xe.
Gia tốc trung bình của một vận động viên chạy nước rút từ khi xuất phát đến khi đạt tốc độ tối đa 9,0 m/s là 6,0 m/. Người ấy tăng tốc trong bao lâu?
Một ô tô tăng tốc từ 5,0 m/s đến 20 m/s trong 6,0 s. Giả sử gia tốc đều, tính quãng đường ô tô đi được trong thời gian này.
Một ô tô đang đi trên đường thẳng với tốc độ v thì trước mặt ô tô đột ngột xuất hiện một mối nguy hiểm. Trong khoảng thời gian từ khi mối nguy xuất hiện đến khi phanh hoạt động, ô tô chuyển động được quãng đường 29,3 m. Khi phanh hoạt động làm bánh xe ngừng quay, các bánh xe của ô tô để lại vết trượt dài 12,8 m trên đường, như hình vẽ. Người ta ước tính rằng trong quá trình trượt, ô tô giảm tốc với gia tốc có độ lớn là 0,85 g, trong đó g là gia tốc rơi tự đo.

a) Xác định:
+ tốc độ v của ô tô trước khi hãm phanh.
+ thời gian từ khi nguy hiểm xuất hiện đến khi phanh hoạt động.
b) Trên một con đường có giới hạn tốc độ cho phép là 60 km/h, sử dụng kết quả ở câu hỏi a) để thảo luận về việc tuân thủ quy định về tốc độ cho phép khi lái ô tô.
Một viên đá được thả rơi không vận tốc đầu. Trong giây cuối cùng trước khi chạm đất, viên đá đã rơi được đoạn đường dài 24,5 m. Lấy g = 9,8 m/. Tính khoảng thời gian rơi tự do của viên đá này.
Tính quãng đường mà vật rơi tự do đi được trong giây thứ tư. Trong khoảng thời gian đó vận tốc của vật đã tăng lên bao nhiêu? Lấy gia tốc rơi tự do g = 9,8 m/.
Thả một hòn đá rơi từ miệng một cái hang sâu xuống đến đáy. Sau 4 s kế từ lúc bắt đầu thả thì nghe tiếng hòn đá chạm vào đáy. Tính chiều sâu của hang. Biết vận tốc truyền âm trong không khí là 330 m/s. Lấy g = 9,8 m/.
Thả một hòn sỏi từ trên gác cao xuống đất. Trong giây cuối cùng hòn sỏi rơi được quãng đường 15 m. Tính độ cao của điểm từ lúc bắt đầu thả rơi hòn sỏi. Lấy g = 9,8 m/.
Một vận động viên ném một quả bóng theo phương thẳng đứng lên trên với tốc độ ban đầu là 18,0 m/s. Cho biết g = 9,81 m/.
a) Quả bóng lên cao bao nhiêu?
b) Sau thời gian bao lâu nó trở về điểm ném?
Từ mái nhà có các giọt nước đang rơi xuống đất. Sau 2 s kể từ lúc giọt nước thứ hai bắt đầu rơi. Khoảng cách giữa giọt nước thứ hai và giọt nước thứ nhất là 25 m. Cho biết giọt nước thứ hai rơi trễ hơn giọt nước thứ nhất bao lâu?
Một nhà du hành vũ trụ trên Mặt Trăng thả một chiếc búa từ độ cao 1,2 m. Búa chạm bề mặt Mặt Trăng sau 1,2 s tính từ khi được thả. Tính độ lớn gia tốc rơi tự do trên Mặt Trăng.
Từ vách núi, người ta thả rơi một hòn đá xuống vực sâu. Từ lúc thả rơi đến lúc nghe tiếng hòn đá chạm đáy vực là 6,5 s. Cho vận tốc truyền âm trong không khí là 360 m/s. Cho g = 10 m/.
a) Tìm thời gian rơi.
b) Khoảng cách từ vách núi đến đáy vực.
Một người có khối lượng 55,0 kg đi trên xe đạp có khối lượng 15,0 kg. Khi xuất phát, hợp lực tác dụng lên xe đạp là 200 N. Giả sử hợp lực tác dụng lên xe đạp không đổi, hãy tính giá trị vận tốc của xe đạp sau 6,00 s.
Một xe lăn có khối lượng 50 kg đang đứng yên trên mặt sàn nằm ngang thì chịu tác dụng bởi một lực kéo không đổi theo phương ngang làm cho xe chuyển động từ đầu phòng đến cuối phòng trong khoảng thời gian 15 s. Nếu người ta đặt lên xe một kiện hàng thì nhận thấy thời gian chuyển động của xe lúc này là 25 s dưới tác dụng của lực trên. Bỏ qua mọi ma sát. Khối lượng của kiện hàng được đặt lên xe là bao nhiêu?
Một chất điểm khối lượng m = 500 g trượt trên mặt phẳng nằm ngang dưới tác dụng của lực kéo theo phương ngang. Cho hệ số ma sát μ = 0,4, lấy g = 10 m/. Đồ thị vận tốc - thời gian của chất điểm như hình vẽ. Xác định giá trị của lực kéo trên mỗi giai đoạn OA, OB và BC.
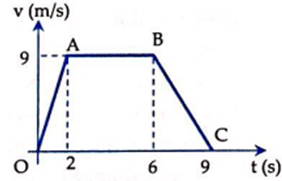
Một vật có khối lượng M = 33 kg được đẩy trên mặt không ma sát bằng 1 thanh sắt có khối lượng m = 3,2 kg. Vật chuyển động (từ trạng thái đứng yên) một đoạn 77 cm trong thời gian 1,7 s với gia tốc không đổi.

a) Hãy chỉ ra các cặp lực - phản lực theo phương ngang.
b) Tay sẽ phải tác dụng lên thanh một lực bằng bao nhiêu?
c) Thanh sắt đẩy vật với một lực bằng bao nhiêu?
d) Hợp lực tác dụng lên thanh sắt bằng bao nhiêu?
Một người đẩy máy cắt cỏ có khối lượng 15,0 kg di chuyển với một lực có độ lớn không đổi bằng 60,0 N theo phương của giá đẩy như hình vẽ. Biết góc tạo bởi giá đây và phương ngang là .

a) Tìm độ lớn của lực đẩy theo phương ngang và phương thẳng đứng.
b) Nếu từ trạng thái nghỉ, người này tác dụng lực để tăng tốc cho máy đạt tốc độ 1,2 m/s trong 3 s thì độ lớn lực ma sát trong giai đoạn này là bao nhiêu?
Hãy giúp Công Thức Vật Lý chọn lọc những nội dung tốt bạn nhé!
hay
và
Thời gian bay trong tụ :
Đồ thị chuyển động thẳng đều trong hệ tọa độ (xOt) là đường thẳng.
Đồ thị vận tốc trong hệ tọa độ (vOt) có dạng đường thẳng.
Đồ thị gia tốc trong hệ tọa độ (aOt) có dạng đường thẳng vuông góc trục gia tốc.
Đồ thị tọa độ trong hệ tọa độ (xOt) có dạng parabol.